题目
计算(int )_(-1)^1sqrt [3]({x)^2}(sin )^5xdx
计算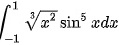
题目解答
答案
因为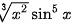
为奇函数，根据定积分的性质，得
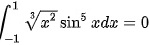
解析
步骤 1：确定函数的奇偶性
函数$f(x) = \sqrt[3]{x^2}\sin^5x$，其中$\sqrt[3]{x^2}$是偶函数，$\sin^5x$是奇函数。偶函数乘以奇函数得到奇函数，因此$f(x)$是奇函数。
步骤 2：应用定积分的性质
根据定积分的性质，如果$f(x)$是奇函数，那么${\int }_{-a}^{a}f(x)dx=0$，其中$a$是任意实数。
步骤 3：计算定积分
由于$f(x) = \sqrt[3]{x^2}\sin^5x$是奇函数，根据定积分的性质，${\int }_{-1}^{1}\sqrt[3]{x^2}\sin^5xdx=0$。
函数$f(x) = \sqrt[3]{x^2}\sin^5x$，其中$\sqrt[3]{x^2}$是偶函数，$\sin^5x$是奇函数。偶函数乘以奇函数得到奇函数，因此$f(x)$是奇函数。
步骤 2：应用定积分的性质
根据定积分的性质，如果$f(x)$是奇函数，那么${\int }_{-a}^{a}f(x)dx=0$，其中$a$是任意实数。
步骤 3：计算定积分
由于$f(x) = \sqrt[3]{x^2}\sin^5x$是奇函数，根据定积分的性质，${\int }_{-1}^{1}\sqrt[3]{x^2}\sin^5xdx=0$。