题目
求极限lim _(narrow infty )dfrac ({2)^n+(3)^n+(7)^n}({5)^n+(8)^n}lim _(narrow infty )dfrac ({2)^n+(3)^n+(7)^n}({5)^n+(8)^n}
求极限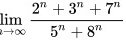
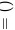
题目解答
答案
对于求极限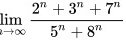
可以观察分子分母,同时除以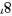
即为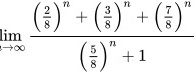
又已知当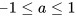 ,在
,在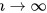 ,
,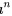
据此可以推出原式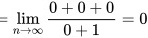
故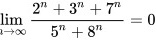
解析
步骤 1:确定主导项
观察分子和分母中的项,可以看到$7^n$和$8^n$是主导项,因为它们的底数最大,随着$n$的增加,它们的增长速度最快。
步骤 2:提取主导项
为了简化极限的计算,我们可以在分子和分母中提取主导项$8^n$,这样可以将极限转换为更易于处理的形式。
步骤 3:计算极限
提取主导项后,分子和分母中的其他项将变为$0$,因为它们的底数小于$8$,随着$n$的增加,它们的值将趋近于$0$。
观察分子和分母中的项,可以看到$7^n$和$8^n$是主导项,因为它们的底数最大,随着$n$的增加,它们的增长速度最快。
步骤 2:提取主导项
为了简化极限的计算,我们可以在分子和分母中提取主导项$8^n$,这样可以将极限转换为更易于处理的形式。
步骤 3:计算极限
提取主导项后,分子和分母中的其他项将变为$0$,因为它们的底数小于$8$,随着$n$的增加,它们的值将趋近于$0$。