题目
下列计算错误的是 ()。A int dfrac (1)(x)dx=ln |x|+C B int dfrac (1)(x)dx=ln |x|+C C int dfrac (1)(x)dx=ln |x|+CD int dfrac (1)(x)dx=ln |x|+C
下列计算错误的是 ()。
A 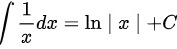
B 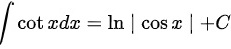
C 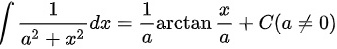
D 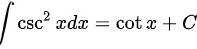
题目解答
答案
解:依次判断;
A:正确;
B: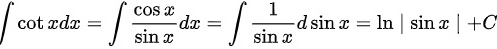 ,B错误;
,B错误;
C: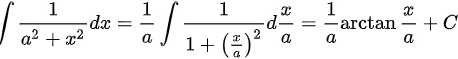 ,C正确;
,C正确;
D: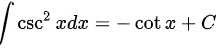 ,D错误。
,D错误。
综上所述:本题选择BD选项。
解析
步骤 1:分析选项A
$\int \dfrac {1}{x}dx=\ln |x|+C$ 是正确的,因为这是基本的积分公式之一。
步骤 2:分析选项B
$\cot xdx=\ln |\cos x|+C$ 是错误的,因为 $\cot xdx$ 的正确积分应该是 $\int \cot xdx = \int \dfrac {\cos x}{\sin x}dx = \ln |\sin x|+C$。
步骤 3:分析选项C
$\int \dfrac {1}{{a}^{2}+{x}^{2}}dx=\dfrac {1}{a}\arctan \dfrac {x}{a}+C(a\neq 0)$ 是正确的,因为这是积分公式 $\int \dfrac {1}{{a}^{2}+{x}^{2}}dx=\dfrac {1}{a}\arctan \dfrac {x}{a}+C$ 的直接应用。
步骤 4:分析选项D
${\csc }^{2}xdx=\cot x+C$ 是错误的,因为 ${\csc }^{2}xdx$ 的正确积分应该是 $\int {\csc }^{2}xdx = -\cot x+C$。
$\int \dfrac {1}{x}dx=\ln |x|+C$ 是正确的,因为这是基本的积分公式之一。
步骤 2:分析选项B
$\cot xdx=\ln |\cos x|+C$ 是错误的,因为 $\cot xdx$ 的正确积分应该是 $\int \cot xdx = \int \dfrac {\cos x}{\sin x}dx = \ln |\sin x|+C$。
步骤 3:分析选项C
$\int \dfrac {1}{{a}^{2}+{x}^{2}}dx=\dfrac {1}{a}\arctan \dfrac {x}{a}+C(a\neq 0)$ 是正确的,因为这是积分公式 $\int \dfrac {1}{{a}^{2}+{x}^{2}}dx=\dfrac {1}{a}\arctan \dfrac {x}{a}+C$ 的直接应用。
步骤 4:分析选项D
${\csc }^{2}xdx=\cot x+C$ 是错误的,因为 ${\csc }^{2}xdx$ 的正确积分应该是 $\int {\csc }^{2}xdx = -\cot x+C$。