题目
1.求下列幂级数的收敛域(或收敛圆):-|||-(1) sum _(n=1)^infty dfrac (1)({2)^n}(x)^2n-1;-|||-(2) sum _(n=1)^infty (n)^2((x+dfrac {1)(2))}^n;-|||-(3) sum _(n=1)^infty dfrac (ln n)(n)(x)^n;-|||-(4) sum _(n=1)^infty dfrac ({(n!))^2}((2n)!)((x-dfrac {1)(4))}^n;-|||-(5) sum _(n=1)^infty dfrac ({(-1))^n}(n+sqrt {n)}(x)^n ;-|||-(6) sum _(n=1)^infty dfrac ({3)^n+((-2))^n}(n)((2x+1))^n;-|||-(7) sum _(n=1)^infty (2)^n(z)^n;-|||-(8) sum _(n=1)^infty dfrac ({n)^2}(n!)((z+1))^n;-|||-(9) sum _(n=1)^infty dfrac (n)({4)^n-1}(z)^2n-|||-(10) sum _(n=1)^infty (n)^n(z)^n.

题目解答
答案
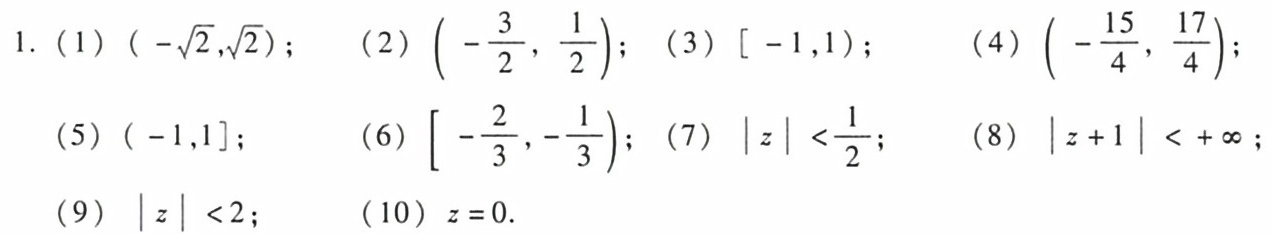
解析
步骤 1:确定收敛半径
对于幂级数 $\sum _{n=1}^{\infty }a_n(x-c)^n$,其收敛半径 $R$ 可以通过比值判别法或根值判别法求得。比值判别法是计算 $\lim_{n\to\infty}|\frac{a_{n+1}}{a_n}|$,根值判别法是计算 $\lim_{n\to\infty}\sqrt[n]{|a_n|}$。收敛半径 $R$ 为上述极限的倒数。
步骤 2:确定收敛区间
收敛区间为 $(c-R, c+R)$,其中 $c$ 是幂级数的中心。需要检查端点处的收敛性。
步骤 3:确定收敛域
根据收敛区间和端点的收敛性,确定幂级数的收敛域。
对于幂级数 $\sum _{n=1}^{\infty }a_n(x-c)^n$,其收敛半径 $R$ 可以通过比值判别法或根值判别法求得。比值判别法是计算 $\lim_{n\to\infty}|\frac{a_{n+1}}{a_n}|$,根值判别法是计算 $\lim_{n\to\infty}\sqrt[n]{|a_n|}$。收敛半径 $R$ 为上述极限的倒数。
步骤 2:确定收敛区间
收敛区间为 $(c-R, c+R)$,其中 $c$ 是幂级数的中心。需要检查端点处的收敛性。
步骤 3:确定收敛域
根据收敛区间和端点的收敛性,确定幂级数的收敛域。