题目
(4) limxcotx;
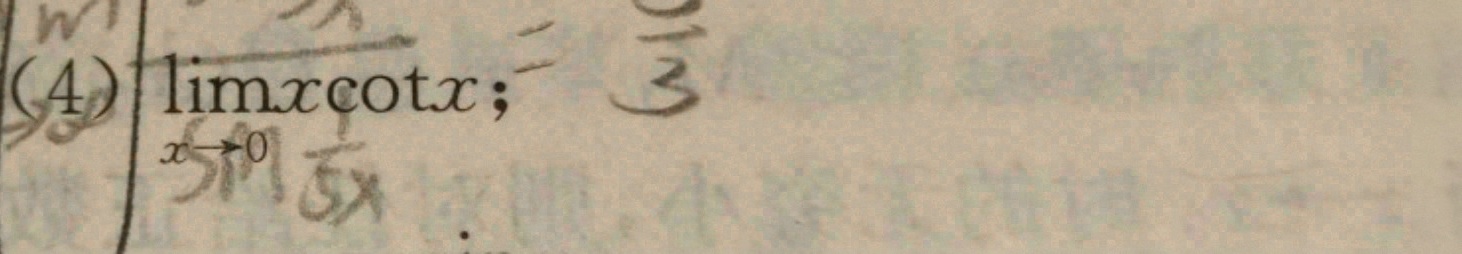
题目解答
答案

解析
考查要点:本题主要考查极限的计算,特别是利用等价无穷小替换或基本三角函数极限性质求解。
解题核心思路:将余切函数$\cot x$转化为$\frac{\cos x}{\sin x}$,结合$x \to 0$时$\sin x \sim x$的等价无穷小替换,简化表达式后直接求极限。
破题关键点:
- 余切函数拆分:$\cot x = \frac{\cos x}{\sin x}$;
- 等价无穷小替换:当$x \to 0$时,$\sin x \sim x$;
- 极限运算性质:乘积的极限等于极限的乘积(当各部分极限存在时)。
将原式$\lim_{x \to 0^+} x \cot x$变形为:
$\lim_{x \to 0^+} x \cdot \frac{\cos x}{\sin x}$
步骤1:拆分表达式
利用$\cot x = \frac{\cos x}{\sin x}$,原式可拆分为:
$\lim_{x \to 0^+} \left( \frac{x}{\sin x} \cdot \cos x \right)$
步骤2:应用等价无穷小替换
当$x \to 0$时,$\sin x \sim x$,因此:
$\frac{x}{\sin x} \to \frac{x}{x} = 1$
步骤3:计算余下部分的极限
$\cos x$在$x=0$处连续,故:
$\lim_{x \to 0^+} \cos x = \cos 0 = 1$
步骤4:结合乘积结果
根据极限的乘积性质:
$\lim_{x \to 0^+} \left( \frac{x}{\sin x} \cdot \cos x \right) = 1 \cdot 1 = 1$