例8】(2022,数三)已知函数 (x)=(e)^sin x+(e)^-sin x, 则 ''(2pi )= __
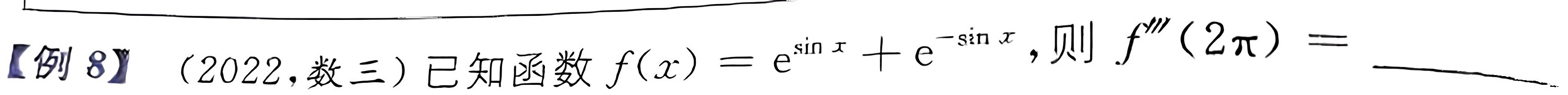
题目解答
答案
[答案]0
解析
考查要点:本题主要考查函数的二阶导数计算,涉及链式法则、乘积法则的应用,以及特殊角三角函数值的计算。
解题思路:
- 求一阶导数:对函数$f(x)=e^{\sin x} + e^{-\sin x}$使用链式法则求导。
- 求二阶导数:对一阶导数结果应用乘积法则,展开后化简。
- 代入$x=2\pi$:利用$\sin 2\pi = 0$和$\cos 2\pi = 1$简化计算。
关键点:
- 链式法则处理复合函数$e^{\sin x}$和$e^{-\sin x}$。
- 乘积法则处理一阶导数中的乘积项。
- 特殊角三角函数值简化最终结果。
步骤1:求一阶导数$f'(x)$
函数$f(x)=e^{\sin x} + e^{-\sin x}$,对每一项分别求导:
- 对$e^{\sin x}$求导:$\cos x \cdot e^{\sin x}$(链式法则)。
- 对$e^{-\sin x}$求导:$-\cos x \cdot e^{-\sin x}$(链式法则)。
因此:
$f'(x) = \cos x \left( e^{\sin x} - e^{-\sin x} \right)$
步骤2:求二阶导数$f''(x)$
对$f'(x)=\cos x \cdot \left( e^{\sin x} - e^{-\sin x} \right)$应用乘积法则:
$f''(x) = \frac{d}{dx}(\cos x) \cdot \left( e^{\sin x} - e^{-\sin x} \right) + \cos x \cdot \frac{d}{dx} \left( e^{\sin x} - e^{-\sin x} \right)$
逐项计算:
-
第一项:$\frac{d}{dx}(\cos x) = -\sin x$,因此第一项为:
$-\sin x \cdot \left( e^{\sin x} - e^{-\sin x} \right)$ -
第二项:对$\left( e^{\sin x} - e^{-\sin x} \right)$求导:
$\cos x \cdot e^{\sin x} + \cos x \cdot e^{-\sin x} = \cos x \cdot \left( e^{\sin x} + e^{-\sin x} \right)$
因此第二项为:
$\cos x \cdot \cos x \cdot \left( e^{\sin x} + e^{-\sin x} \right) = \cos^2 x \cdot \left( e^{\sin x} + e^{-\sin x} \right)$
综上,二阶导数为:
$f''(x) = -\sin x \cdot \left( e^{\sin x} - e^{-\sin x} \right) + \cos^2 x \cdot \left( e^{\sin x} + e^{-\sin x} \right)$
步骤3:代入$x=2\pi$
利用$\sin 2\pi = 0$和$\cos 2\pi = 1$:
- 第一项:$-\sin 2\pi \cdot \left( e^{\sin 2\pi} - e^{-\sin 2\pi} \right) = 0$。
- 第二项:$\cos^2 2\pi \cdot \left( e^{\sin 2\pi} + e^{-\sin 2\pi} \right) = 1^2 \cdot (1 + 1) = 2$。
因此:
$f''(2\pi) = 0 + 2 = 2$