题目
6、把一些橙和柑分装入袋,如果每袋6个橙、5个柑,橙分完了还剩3个柑;如果每袋8个柑、6个橙,柑分 完了还剩18个橙.橙和柑一共有多少个?
6、把一些橙和柑分装入袋,如果每袋6个橙、5个柑,橙分完了还剩3个柑;如果每袋8个柑、6个橙,柑分
完了还剩18个橙.橙和柑一共有多少个?
完了还剩18个橙.橙和柑一共有多少个?
题目解答
答案
设橙X,柑Y
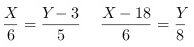
解得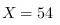 ,
,
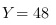
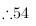 个橙,48个柑
个橙,48个柑
橙和柑一共有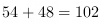
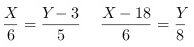
解得
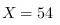 ,
,
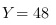
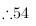 个橙,48个柑
个橙,48个柑
橙和柑一共有
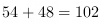
解析
考查要点:本题属于分组问题,需要根据两种不同的分装方式建立方程,求解橙和柑的数量。关键在于理解分装过程中袋数与剩余数量的关系。
解题核心思路:
- 设定变量:设橙的数量为$x$,柑的数量为$y$。
- 建立方程:
- 第一种分装方式下,橙分完时柑剩余3个,袋数由橙的数量决定。
- 第二种分装方式下,柑分完时橙剩余18个,袋数由柑的数量决定。
- 联立方程:通过袋数的关联关系,建立两个方程并求解。
破题关键点:
- 袋数的统一:两种分装方式的袋数不同,需通过变量表达袋数。
- 剩余数量的处理:剩余的柑或橙需体现在方程中。
设定变量
设橙的数量为$x$,柑的数量为$y$。
第一种分装方式
- 每袋装6个橙,分完橙的袋数为$\dfrac{x}{6}$。
- 每袋装5个柑,分完后剩余3个柑,因此柑的总数为$5 \times \dfrac{x}{6} + 3$。
- 方程:
$y = \dfrac{5x}{6} + 3 \quad \text{(1)}$
第二种分装方式
- 每袋装8个柑,分完柑的袋数为$\dfrac{y}{8}$。
- 每袋装6个橙,分完后剩余18个橙,因此橙的总数为$6 \times \dfrac{y}{8} + 18$。
- 方程:
$x = \dfrac{6y}{8} + 18 \quad \text{(2)}$
联立方程求解
-
整理方程:
- 方程(1):$6y = 5x + 18$ → $5x - 6y = -18$
- 方程(2):$8x = 6y + 144$ → $4x - 3y = 72$
-
消元法:
- 将第二个方程乘以2:$8x - 6y = 144$
- 减去第一个方程:$(8x - 6y) - (5x - 6y) = 144 - (-18)$
- 得:$3x = 162$ → $x = 54$
-
代入求$y$:
- 代入$x = 54$到$4x - 3y = 72$:
$4 \times 54 - 3y = 72$ → $216 - 3y = 72$ → $y = 48$
- 代入$x = 54$到$4x - 3y = 72$: