9.设二维随机变量(X,Y)的概率密度为-|||-,-|||-f(x,y)= ) c(x)^2y, (x)^2leqslant yleqslant 1 0, .-|||-(1)确定常数c.-|||-(2)求边缘概率密度.

步骤 1：确定常数c
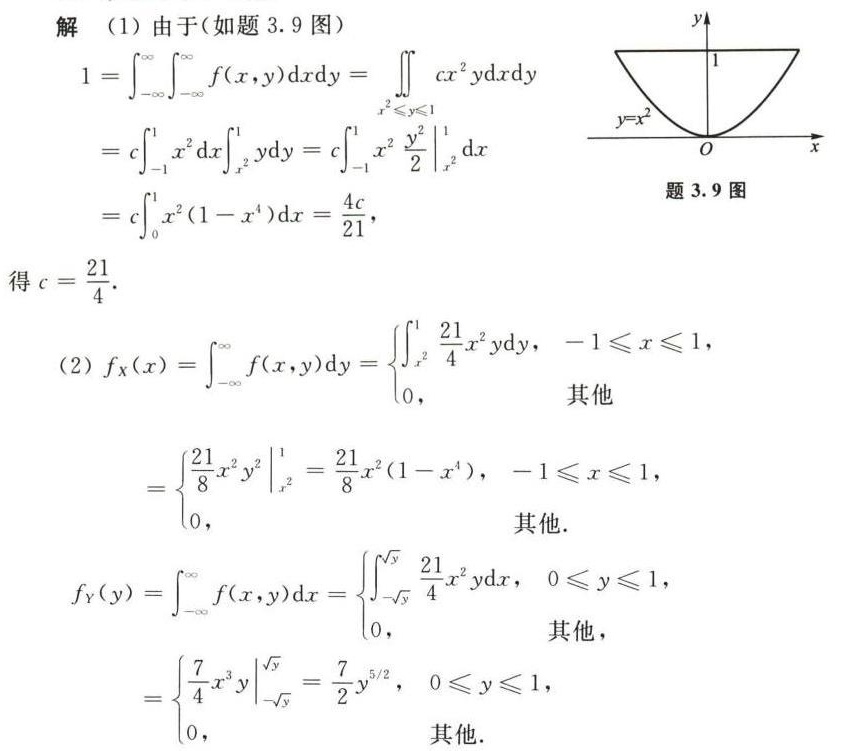
为了确定常数c，我们需要利用概率密度函数的性质，即整个区域上的积分等于1。因此，我们首先计算积分：
$$
\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} f(x,y) \, dy \, dx = 1
$$
由于f(x,y)在${x}^{2}\leqslant y\leqslant 1$的范围内非零，我们只需要在这个范围内进行积分。因此，积分变为：
$$
\int_{-1}^{1}\int_{x^2}^{1} c{x}^{2}y \, dy \, dx = 1
$$
步骤 2：计算积分
我们首先对y进行积分，然后对x进行积分：
$$
\int_{-1}^{1}\int_{x^2}^{1} c{x}^{2}y \, dy \, dx = c\int_{-1}^{1}{x}^{2}\left[\frac{y^2}{2}\right]_{x^2}^{1} \, dx = c\int_{-1}^{1}{x}^{2}\left(\frac{1}{2} - \frac{x^4}{2}\right) \, dx
$$
$$
= \frac{c}{2}\int_{-1}^{1}{x}^{2} - {x}^{6} \, dx = \frac{c}{2}\left[\frac{x^3}{3} - \frac{x^7}{7}\right]_{-1}^{1} = \frac{c}{2}\left(\frac{2}{3} - \frac{2}{7}\right) = \frac{c}{2}\left(\frac{14 - 6}{21}\right) = \frac{c}{2}\left(\frac{8}{21}\right) = \frac{4c}{21}
$$
步骤 3：求解c
由于整个区域上的积分等于1，我们有：
$$
\frac{4c}{21} = 1
$$
解得：
$$
c = \frac{21}{4}
$$
步骤 4：求边缘概率密度
边缘概率密度${f}_{x}(x)$和${f}_{Y}(y)$分别通过积分f(x,y)得到：
$$
{f}_{x}(x) = \int_{-\infty}^{\infty} f(x,y) \, dy = \int_{x^2}^{1} \frac{21}{4}{x}^{2}y \, dy = \frac{21}{4}{x}^{2}\left[\frac{y^2}{2}\right]_{x^2}^{1} = \frac{21}{8}{x}^{2}(1 - x^4)
$$
$$
{f}_{Y}(y) = \int_{-\infty}^{\infty} f(x,y) \, dx = \int_{-\sqrt{y}}^{\sqrt{y}} \frac{21}{4}{x}^{2}y \, dx = \frac{21}{4}y\left[\frac{x^3}{3}\right]_{-\sqrt{y}}^{\sqrt{y}} = \frac{7}{2}y^{5/2}
$$