题目
讨论函数(x)=lim _(narrow infty )dfrac (1-{x)^2n}(1+{x)^2n}x的连续性,若有间断点,判别其类型 .
讨论函数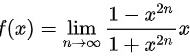 的连续性,若有间断点,判别其类型 .
的连续性,若有间断点,判别其类型 .
题目解答
答案
对于函数
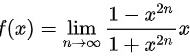
其分母不能为零
则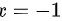 是函数的间断点
是函数的间断点
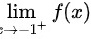
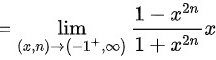
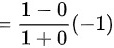
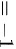
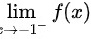
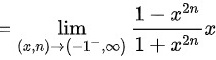
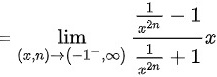
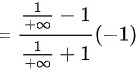
则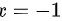 的两侧极限都存在但不相等
的两侧极限都存在但不相等
即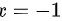 是函数的跳跃间断点
是函数的跳跃间断点
解析
考查要点:本题主要考查函数极限的计算、分段函数的连续性判断以及间断点类型的判定。
解题核心思路:
- 分情况讨论:根据$x$的不同取值范围($|x| < 1$、$|x| > 1$、$|x| = 1$),分别计算极限表达式$\dfrac{1 - x^{2n}}{1 + x^{2n}}$的值。
- 确定分段表达式:结合极限结果与$x$,得到函数$f(x)$的分段形式。
- 连续性分析:在分段点$x = \pm 1$处,计算左右极限并与函数值比较,判断是否存在间断点及其类型。
破题关键点:
- 极限计算:利用$|x| < 1$时$x^{2n} \to 0$,$|x| > 1$时$x^{2n} \to +\infty$的性质简化分式。
- 分段点分析:特别关注$x = \pm 1$处的左右极限与函数值的关系。
步骤1:分情况讨论极限表达式
-
当$|x| < 1$时:
$x^{2n} \to 0$,分式$\dfrac{1 - x^{2n}}{1 + x^{2n}} \to \dfrac{1 - 0}{1 + 0} = 1$,故$f(x) = 1 \cdot x = x$。 -
当$|x| > 1$时:
$x^{2n} \to +\infty$,分式可变形为$\dfrac{\frac{1}{x^{2n}} - 1}{\frac{1}{x^{2n}} + 1} \to \dfrac{0 - 1}{0 + 1} = -1$,故$f(x) = -1 \cdot x = -x$。 -
当$|x| = 1$时:
- 若$x = 1$或$x = -1$,则$x^{2n} = 1$,分式$\dfrac{1 - 1}{1 + 1} = 0$,故$f(x) = 0 \cdot x = 0$。
步骤2:分析连续性
-
在$|x| < 1$和$|x| > 1$区间内:
$f(x)$分别由$x$和$-x$表示,均为连续函数,故无间断点。 -
在$x = 1$处:
- 左极限($x \to 1^-$):$f(x) = x \to 1$。
- 右极限($x \to 1^+$):$f(x) = -x \to -1$。
- 函数值:$f(1) = 0$。
左右极限存在但不相等,且均不等于$f(1)$,故$x = 1$为跳跃间断点。
-
在$x = -1$处:
- 右极限($x \to -1^+$):$f(x) = x \to -1$。
- 左极限($x \to -1^-$):$f(x) = -x \to 1$。
- 函数值:$f(-1) = 0$。
左右极限存在但不相等,且均不等于$f(-1)$,故$x = -1$为跳跃间断点。