题目
22.设X和Y是两个相互独立的随机变量,其概率密度分别为-|||-_(x)(x)= ) 1, 0leqslant xleqslant 1 0, 其他, .-|||-, ,-|||-求随机变量 =X+Y 的概率密度.

题目解答
答案
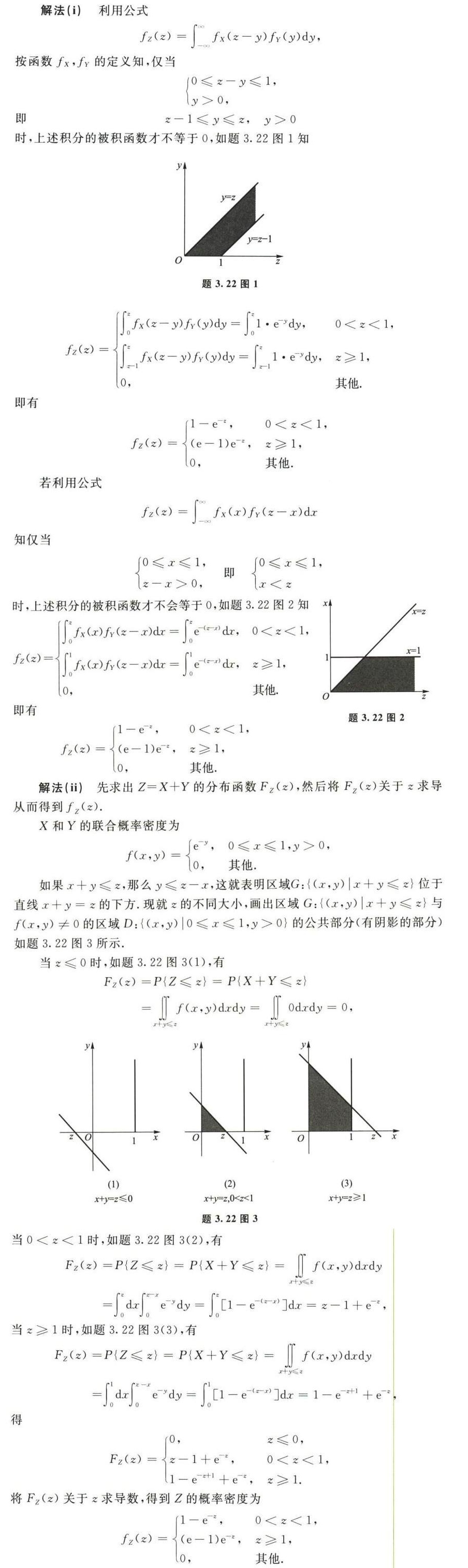
解析
考查要点:本题主要考查两个独立随机变量和的卷积公式应用,需要根据变量的取值范围分段讨论积分区间。
解题核心思路:
- 独立随机变量的卷积公式:利用$f_Z(z) = \int_{-\infty}^{+\infty} f_X(x) f_Y(z-x) \, dx$,结合X和Y的定义域确定积分上下限。
- 分段讨论:根据$z$的不同取值范围($z < 0$,$0 \leq z < 1$,$z \geq 1$),分析$x$的合法取值范围,从而确定积分区间。
- 指数函数积分:对含$e^{-y}$的积分进行计算,注意代数变形和积分结果的化简。
破题关键点:
- X的取值范围:$0 \leq x \leq 1$,限制$x$的积分下限和上限。
- Y的取值范围:$y > 0$,即$z - x > 0$,进一步限制$x < z$。
- 分段条件:当$z < 1$时,$x$的上限由$z$决定;当$z \geq 1$时,$x$的上限由$1$决定。
步骤1:确定积分区间
根据$X$和$Y$的定义域,$x$需满足:
- $0 \leq x \leq 1$(来自$f_X(x)$的非零区域);
- $z - x > 0$(来自$f_Y(z-x)$的非零区域),即$x < z$。
因此,积分区间需分情况讨论:
- 当$z < 0$时:无解,$f_Z(z) = 0$;
- 当$0 \leq z < 1$时:$x$的范围是$0 \leq x \leq z$;
- 当$z \geq 1$时:$x$的范围是$0 \leq x \leq 1$。
步骤2:分段计算积分
情况1:$0 \leq z < 1$
积分区间为$0 \leq x \leq z$:
$\begin{aligned}f_Z(z) &= \int_{0}^{z} f_X(x) f_Y(z-x) \, dx \\&= \int_{0}^{z} 1 \cdot e^{-(z-x)} \, dx \\&= e^{-z} \int_{0}^{z} e^{x} \, dx \\&= e^{-z} \left( e^{z} - 1 \right) \\&= 1 - e^{-z}.\end{aligned}$
情况2:$z \geq 1$
积分区间为$0 \leq x \leq 1$:
$\begin{aligned}f_Z(z) &= \int_{0}^{1} 1 \cdot e^{-(z-x)} \, dx \\&= e^{-z} \int_{0}^{1} e^{x} \, dx \\&= e^{-z} \left( e^{1} - 1 \right) \\&= (e - 1) e^{-z}.\end{aligned}$
情况3:$z < 0$
显然无解,$f_Z(z) = 0$。