题目
设随机变量×在×上服从均匀分布，则×1、正确2、错误
设随机变量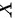
在
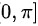上服从均匀分布，则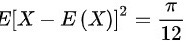
1、正确
2、错误
题目解答
答案
解：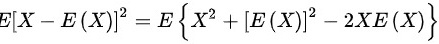
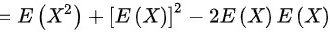
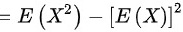
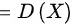
所以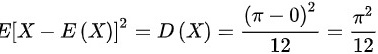
所以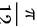
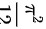不正确，
正确。
解析
步骤 1：计算期望值E(X)
随机变量X在区间$(0,\pi]$上服从均匀分布，其概率密度函数为$f(x) = \frac{1}{\pi}$。期望值E(X)的计算公式为：
$$E(X) = \int_{0}^{\pi} x \cdot f(x) dx = \int_{0}^{\pi} x \cdot \frac{1}{\pi} dx$$
步骤 2：计算方差D(X)
方差D(X)的计算公式为：
$$D(X) = E(X^2) - [E(X)]^2$$
其中，$E(X^2)$的计算公式为：
$$E(X^2) = \int_{0}^{\pi} x^2 \cdot f(x) dx = \int_{0}^{\pi} x^2 \cdot \frac{1}{\pi} dx$$
步骤 3：计算${[ {X}^{X}-E(X)] }^{2}$
根据方差的定义，${[ {X}^{X}-E(X)] }^{2}$等于方差D(X)。
随机变量X在区间$(0,\pi]$上服从均匀分布，其概率密度函数为$f(x) = \frac{1}{\pi}$。期望值E(X)的计算公式为：
$$E(X) = \int_{0}^{\pi} x \cdot f(x) dx = \int_{0}^{\pi} x \cdot \frac{1}{\pi} dx$$
步骤 2：计算方差D(X)
方差D(X)的计算公式为：
$$D(X) = E(X^2) - [E(X)]^2$$
其中，$E(X^2)$的计算公式为：
$$E(X^2) = \int_{0}^{\pi} x^2 \cdot f(x) dx = \int_{0}^{\pi} x^2 \cdot \frac{1}{\pi} dx$$
步骤 3：计算${[ {X}^{X}-E(X)] }^{2}$
根据方差的定义，${[ {X}^{X}-E(X)] }^{2}$等于方差D(X)。