题目
函数=sqrt (3-x)+arctan dfrac (1)(x)的定义域为_________.
函数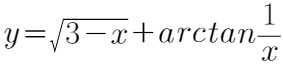
的定义域为_________.
题目解答
答案
{
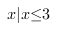且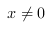
}
解析
步骤 1：确定根号内的表达式
根号内的表达式$3-x$必须大于等于0，即$3-x\geqslant 0$，解得$x\leqslant 3$。
步骤 2：确定arctan函数的定义域
arctan函数的定义域为全体实数，但$\dfrac{1}{x}$要求$x\neq 0$，因为分母不能为0。
步骤 3：综合两个条件
综合以上两个条件，函数$y=\sqrt {3-x}+\arctan \dfrac {1}{x}$的定义域为$x\leqslant 3$且$x\neq 0$。
根号内的表达式$3-x$必须大于等于0，即$3-x\geqslant 0$，解得$x\leqslant 3$。
步骤 2：确定arctan函数的定义域
arctan函数的定义域为全体实数，但$\dfrac{1}{x}$要求$x\neq 0$，因为分母不能为0。
步骤 3：综合两个条件
综合以上两个条件，函数$y=\sqrt {3-x}+\arctan \dfrac {1}{x}$的定义域为$x\leqslant 3$且$x\neq 0$。