题目
已知复数a=3+4i,复试b=4+3i,则a+b的相位可以为()A.45°A.45°A.45°A.45°
已知复数a=3+4i,复试b=4+3i,则a+b的相位可以为()
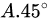
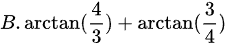
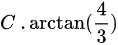
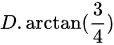
题目解答
答案
答案:A
解析:a+b=(3+4i)+(4+3i)=7+7i
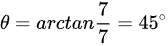
解析
步骤 1:计算复数a和b的和
复数a=3+4i,复数b=4+3i,将它们相加得到a+b=(3+4i)+(4+3i)=7+7i。
步骤 2:确定复数a+b的相位
复数a+b=7+7i,其相位θ可以通过计算$\tan(\theta)=\dfrac{Imaginary\ part}{Real\ part}=\dfrac{7}{7}=1$得到。因此,$\theta=\arctan(1)=45°$。
步骤 3:验证选项
选项A:45°,与计算结果一致。
选项B:$\arctan(\dfrac{4}{3})+\arctan(\dfrac{3}{4})$,不等于45°。
选项C:$\arctan(\dfrac{4}{3})$,不等于45°。
选项D:$\arctan(\dfrac{3}{4})$,不等于45°。
复数a=3+4i,复数b=4+3i,将它们相加得到a+b=(3+4i)+(4+3i)=7+7i。
步骤 2:确定复数a+b的相位
复数a+b=7+7i,其相位θ可以通过计算$\tan(\theta)=\dfrac{Imaginary\ part}{Real\ part}=\dfrac{7}{7}=1$得到。因此,$\theta=\arctan(1)=45°$。
步骤 3:验证选项
选项A:45°,与计算结果一致。
选项B:$\arctan(\dfrac{4}{3})+\arctan(\dfrac{3}{4})$,不等于45°。
选项C:$\arctan(\dfrac{4}{3})$,不等于45°。
选项D:$\arctan(\dfrac{3}{4})$,不等于45°。