题目
已知向量组0 underline (1) -1 1 3-|||-A:a1= 1 a2= 1 :B:(b)_(1)= 0 b2= 2 ,b3= 2-|||-1 0 underline (1) 1 -1证明向量组0 underline (1) -1 1 3-|||-A:a1= 1 a2= 1 :B:(b)_(1)= 0 b2= 2 ,b3= 2-|||-1 0 underline (1) 1 -1与向量组0 underline (1) -1 1 3-|||-A:a1= 1 a2= 1 :B:(b)_(1)= 0 b2= 2 ,b3= 2-|||-1 0 underline (1) 1 -1等价.
已知向量组
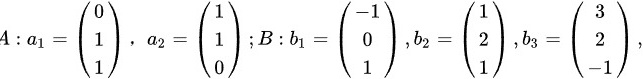 证明向量组
证明向量组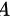 与向量组
与向量组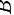 等价.
等价.
题目解答
答案
解:令 则
则
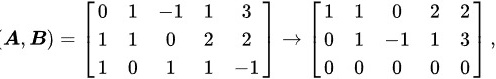 所以
所以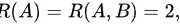 而B有二阶子式
而B有二阶子式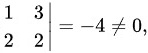 所以
所以 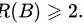 另外
另外
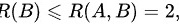 所以
所以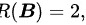 从而有
从而有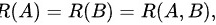 所以
所以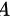 组与
组与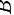 组等价.
组等价.
解析
步骤 1:构造矩阵
构造矩阵$A=({a}_{1},{a}_{2})$和$B=({b}_{1},{b}_{2},{b}_{3})$,其中${a}_{1},{a}_{2}$是向量组的向量,${b}_{1},{b}_{2},{b}_{3}$是向量组的向量。
步骤 2:构造增广矩阵
构造增广矩阵$(A,B)$,并进行初等行变换,以简化矩阵。
步骤 3:计算秩
计算矩阵$A$、增广矩阵$(A,B)$和矩阵$B$的秩,以确定向量组的线性相关性。
步骤 4:验证等价性
根据秩的计算结果,验证向量组与向量组的等价性。
构造矩阵$A=({a}_{1},{a}_{2})$和$B=({b}_{1},{b}_{2},{b}_{3})$,其中${a}_{1},{a}_{2}$是向量组的向量,${b}_{1},{b}_{2},{b}_{3}$是向量组的向量。
步骤 2:构造增广矩阵
构造增广矩阵$(A,B)$,并进行初等行变换,以简化矩阵。
步骤 3:计算秩
计算矩阵$A$、增广矩阵$(A,B)$和矩阵$B$的秩,以确定向量组的线性相关性。
步骤 4:验证等价性
根据秩的计算结果,验证向量组与向量组的等价性。