题目
[题目]设区域 = (x,y)|{x)^2+(y)^2leqslant 1,xgeqslant 0} , 计算二重-|||-积分 int Ddfrac (1+xy)(1+{x)^2+(y)^2} dxdy.
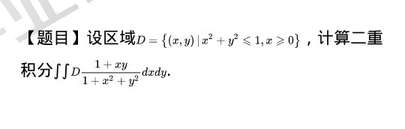
题目解答
答案

解析
考查要点:本题主要考查二重积分的对称性应用及极坐标变换法。
解题核心思路:
- 拆分被积函数:将积分拆分为两个部分,利用对称性简化计算。
- 对称性分析:观察到被积函数中的$xy$项在对称区域上的积分为零。
- 极坐标变换:将剩余部分转换为极坐标,简化积分计算。
破题关键点:
- 对称性判断:区域$D$关于$y$轴对称,$xy$为奇函数,积分结果为零。
- 极坐标转换:利用极坐标下$x^2 + y^2 = r^2$的特性,简化分母表达式。
步骤1:拆分被积函数
将原积分拆分为两部分:
$\iint_D \frac{1+xy}{1+x^2+y^2} \,dx\,dy = \iint_D \frac{1}{1+x^2+y^2} \,dx\,dy + \iint_D \frac{xy}{1+x^2+y^2} \,dx\,dy.$
步骤2:利用对称性简化
- 分析$\iint_D \frac{xy}{1+x^2+y^2} \,dx\,dy$:
区域$D$关于$y$轴对称,对任意$(x,y) \in D$,点$(x,-y) \in D$。
由于$xy$在$y$方向为奇函数,积分结果为$0$。
步骤3:极坐标变换
- 转换$\iint_D \frac{1}{1+x^2+y^2} \,dx\,dy$:
区域$D$在极坐标下表示为$r \in [0,1]$,$\theta \in [-\frac{\pi}{2}, \frac{\pi}{2}]$,雅可比行列式为$r$。
积分变为:
$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \int_0^1 \frac{1}{1+r^2} \cdot r \,dr\,d\theta.$
步骤4:计算积分
- 对$r$积分:
$\int_0^1 \frac{r}{1+r^2} \,dr = \frac{1}{2} \ln(1+r^2) \Big|_0^1 = \frac{1}{2} \ln 2.$ - 对$\theta$积分:
$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} d\theta = \pi.$ - 最终结果:
$\pi \cdot \frac{1}{2} \ln 2 = \frac{\pi}{2} \ln 2.$