题目
已知 (x+1)=(x)^2+1, 则 f(x)= __
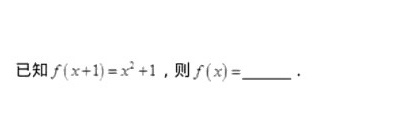
题目解答
答案
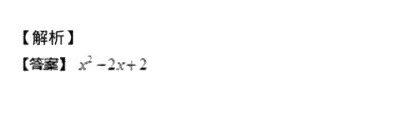
解析
步骤 1:代换变量
为了求出 $f(x)$,我们首先需要将 $f(x+1)$ 中的 $x$ 替换为 $x-1$,这样可以将 $f(x+1)$ 转换为 $f(x)$ 的形式。这是因为 $f(x+1)$ 中的 $x$ 实际上是 $f(x)$ 中的 $x-1$。
步骤 2:替换并计算
将 $x$ 替换为 $x-1$,我们得到 $f(x) = (x-1)^2 + 1$。接下来,我们需要展开这个表达式。
步骤 3:展开表达式
$(x-1)^2 + 1 = x^2 - 2x + 1 + 1 = x^2 - 2x + 2$。
为了求出 $f(x)$,我们首先需要将 $f(x+1)$ 中的 $x$ 替换为 $x-1$,这样可以将 $f(x+1)$ 转换为 $f(x)$ 的形式。这是因为 $f(x+1)$ 中的 $x$ 实际上是 $f(x)$ 中的 $x-1$。
步骤 2:替换并计算
将 $x$ 替换为 $x-1$,我们得到 $f(x) = (x-1)^2 + 1$。接下来,我们需要展开这个表达式。
步骤 3:展开表达式
$(x-1)^2 + 1 = x^2 - 2x + 1 + 1 = x^2 - 2x + 2$。