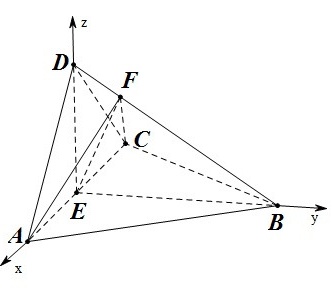
18.(12分)-|||-如图,四面体ABC D中, bot CD , =CD,-|||-angle ADB=angle BDC, E为AC的中点.-|||-(1)证明:平面 bot 平面ACD;-|||-(2)设 AB=BD=2 . angle ACB=(60)^circ , 点F在BD上;-|||-当 Delta AFC 的面积最小时,求CF与平面ABD所成的角的正-|||-弦值.-|||-D-|||-F-|||-1-|||-B-|||-A

题目解答
答案
【答案】
$\left(1\right)$见解析;$\left(2\right)$$\dfrac{4\sqrt{3}}{7}$
【解析】
$\left(1\right)$$\because AD=CD$,$E$为$AC$的中点,
$\therefore DE\bot AC$.
$\because AD=CD$,$\angle ADB=\angle BDC$,$BD=BD$,
$\therefore \triangle ABD\ykcong \triangle CBD$,
$\therefore AB=CB$.
又$\because $$E$为$AC$的中点,
$\therefore BE\bot AC$.
又$\because DE\cap BE=E$,$DE$,$BE\subset $平面$BED$,
$\therefore AC\bot $平面$BED$.
$\because AC\subset $平面$ACD$,
$\therefore $平面$ACD\bot $平面$BED$.
$\left(2\right)$$\because AD=CD$,$\angle ADB=\angle BDC$,$DF=DF$,
$\therefore \triangle AFD\ykcong \triangle CFD$,
$\therefore AF=CF$.
连接$EF$.
$\because E$为$AC$的中点,
$\therefore EF\bot AC$.
由$\left(1\right)$可知$AB=CB$.
又$\because \angle ACB={60}^{\circ }$,$AB=2$,
$\therefore \triangle ABC$为边长为$2$的等边三角形,
$\therefore AC=2$,
$BE=AB\sin {60}^{\circ }=2\times \dfrac{\sqrt{3}}{2}=\sqrt{3}$.
$\because AD\bot CD$,$E$为$AC$的中点,
$\therefore DE=\dfrac{1}{2}AC=\dfrac{1}{2}\times 2=1$,
$\therefore D{E}^{2}+B{E}^{2}=B{D}^{2}$,
$\therefore DE\bot BE$,
$\therefore {S}_{\triangle AFC}=\dfrac{1}{2}AC\cdot EF=\dfrac{1}{2}\times 2\cdot EF=EF$.
要使得$\triangle AFC$的面积最小,只需$EF$最小,即$EF\bot BD$.
此时在$Rt\triangle BED$中,$EF=\dfrac{BE\cdot DE}{BD}=\dfrac{\sqrt{3}\times 1}{2}=\dfrac{\sqrt{3}}{2}$,
则$DF=\sqrt{D{E}^{2}-E{F}^{2}}=\sqrt{{1}^{2}-{\left(\dfrac{\sqrt{3}}{2}\right)}^{2}}=\dfrac{1}{2}$,
故$DF=\dfrac{1}{4}DB$.
$\because DE\bot AC$,$DE\bot BE$,$AC\cap BE=E$,$AC$,$BE\subset $平面$ABC$,
$\therefore DE\bot $平面$ABC$.
以$E$为坐标原点,$EA$,$EB$,$ED$所在直线分别为$x$轴,$y$轴,$z$轴,
建立如图所示空间直角坐标系,
则$A\left(1,0,0\right)$,$B\left(0,\sqrt{3},0\right)$,$C\left(-1,0,0\right)$,$D\left(0,0,1\right)$,
则$\overrightarrow{AB}=\left(-1,\sqrt{3},0\right)$,$\overrightarrow{AD}=\left(-1,0,1\right)$.
设平面$ABD$的法向量为$\overrightarrow{a}=\left(x,y,z\right)$,
则$\left\{\begin{array}{l}\overrightarrow{AB}\cdot \overrightarrow{a}=-x+\sqrt{3}y=0\\ \overrightarrow{AD}\cdot \overrightarrow{a}=-x+z=0\end{array}\right.$
不妨取$y=1$,则$x=z=\sqrt{3}$,故$\overrightarrow{a}=\left(\sqrt{3},1,\sqrt{3}\right)$.
$\overrightarrow{CF}=\overrightarrow{CD}+\overrightarrow{DF}=\overrightarrow{CD}+\dfrac{1}{4}\overrightarrow{DB}$
$=\left(1,0,1\right)+\dfrac{1}{4}\left(0,\sqrt{3},-1\right)=\left(1,\dfrac{\sqrt{3}}{4},\dfrac{3}{4}\right)$.
设$CF$与平面$ABD$所成角的大小为$\theta $,
则$\sin \theta =\left|\cos \lt \overrightarrow{CF},\overrightarrow{a}\gt \right|=\dfrac{\left|\overrightarrow{CF}\cdot \overrightarrow{a}\right|}{\left|\overrightarrow{CF}\right|\cdot \left|\overrightarrow{a}\right|}$
$=\dfrac{\left|1\times \sqrt{3}+\frac{\sqrt{3}}{4}\times 1+\frac{3}{4}\times \sqrt{3}\right|}{\sqrt{{1}^{2}+{\left(\frac{\sqrt{3}}{4}\right)}^{2}+{\left(\frac{3}{4}\right)}^{2}}\times \sqrt{{\left(\sqrt{3}\right)}^{2}+{1}^{2}+{\left(\sqrt{3}\right)}^{2}}}$
$=\dfrac{4\sqrt{3}}{7}$,
即$CF$与平面$ABD$所成角的正弦值为$\dfrac{4\sqrt{3}}{7}$.
解析
考察知识
本题主要考察立体几何中的面面垂直证明、三角形面积最值问题以及线面角的计算,涉及全等三角形、线面垂直判定定理、空间直角坐标系、法向量等知识。
(1)证明:平面$BED\bot$平面$ACD$
解题思路:要证面面垂直,需证一个平面内有一条直线垂直于另一个平面。
- 步骤1:证$AC\bot$平面$BED$
- 因为$AD=CD$,$E$为$AC$中点,根据等腰三角形三线合一,得$DE\bot AC$。
- 由$\angle ADB=\angle BDC$,$BD=BD$,$AD=CD$,得$\triangle ABD\cong\triangle CBD$(SAS),故$AB=CB$。
- 同理,$E$为$AC$中点,得$BE\bot AC$。
- $DE\cap BE=E$,且$DE,BE\subset$平面$BED$,根据线面垂直判定定理,$AC\bot$平面$BED$。
- 步骤2:证面面垂直
$AC\subset$平面$ACD$,且$AC\bot$平面$BED$,根据面面垂直判定定理,平面$ACD\bot$平面$BED$。
(2)求$CF$与平面$ABD$所成角的正弦值
解题思路:先求$\triangle AFC$面积最小时的$F$位置,再用空间向量计算线面角。
- 步骤1:确定$\triangle AFC$面积最小条件
- 由$\triangle ABD\cong\triangle CBD$,得$AF=CF$,$\triangle AFC$为等腰三角形,$S_{\triangle AFC}=\frac{1}{2}AC\cdot EF$($EF\perp AC$)。
- 要使面积最小,需$EF$最小,即$EF\perp BD$($EF$为$Rt\triangle BED$斜边上的高)。
- 步骤2:计算关键长度
- $\triangle ABC$为等边三角形($AB=CB=2$,$\angle ACB=60^\circ$),故$AC=2$,$BE=\sqrt{3}$,$DE=1$(直角三角形斜边中线)。
- $EF=\frac{BE\cdot DE}{BD}=\frac{\sqrt{3}\times1}{2}=\frac{\sqrt{3}}{2}$,$DF=\frac{1}{2}$($Rt\triangle DEF$勾股定理)。
- 步骤3:建立坐标系与向量计算
- 以$E$为原点,$EA,EB,ED$为$x,y,z$轴,得坐标:$A(1,0,0)$,$B(0,\sqrt{3},0)$,$D(0,0,1)$,$F$在$BD$上,$\overrightarrow{DF}=\frac{1}{4}\overrightarrow{DB}$,故$F(1,\frac{\sqrt{3}}{4},\frac{3}{4})$。
- 平面$ABD$的法向量$\overrightarrow{a}=(\sqrt{3},1,\sqrt{3})$(由$\overrightarrow{AB}\cdot\overrightarrow{a}=0$,$\overrightarrow{AD}\cdot\overrightarrow{a}=0$解得)。
- 线面角正弦值$\sin\theta=|\cos\langle\overrightarrow{CF},\overrightarrow{a}\rangle|=\frac{|\overrightarrow{CF}\cdot\overrightarrow{a}|}{|\overrightarrow{CF}|\cdot|\overrightarrow{a}|}=\frac{4\sqrt{3}}{7}$。