题目
4.设随机变量X的分布函数 F(x)= , 0leqslant xlt 1-{e)^-x, xgeqslant 1,
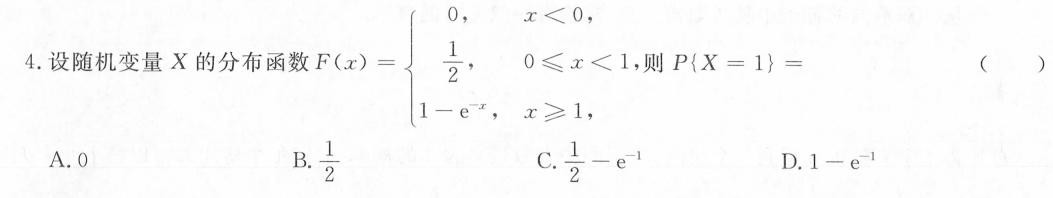
题目解答
答案
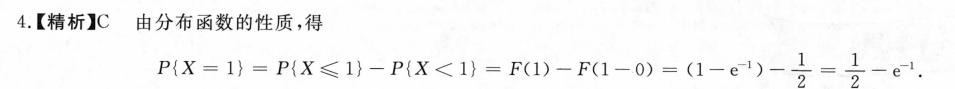
解析
步骤 1:理解分布函数的性质
分布函数F(x)在x处的值表示随机变量X小于等于x的概率,即$P(X \leq x) = F(x)$。对于离散点x=1,$P(X=1)$可以通过分布函数的跳跃来计算,即$P(X=1) = F(1) - \lim_{x \to 1^-} F(x)$。
步骤 2:计算$P(X=1)$
根据题目给出的分布函数F(x),当$x=1$时,$F(1) = 1 - e^{-1}$。而当$x$接近1但小于1时,$F(x) = \frac{1}{2}$。因此,$P(X=1) = F(1) - \lim_{x \to 1^-} F(x) = (1 - e^{-1}) - \frac{1}{2} = \frac{1}{2} - e^{-1}$。
分布函数F(x)在x处的值表示随机变量X小于等于x的概率,即$P(X \leq x) = F(x)$。对于离散点x=1,$P(X=1)$可以通过分布函数的跳跃来计算,即$P(X=1) = F(1) - \lim_{x \to 1^-} F(x)$。
步骤 2:计算$P(X=1)$
根据题目给出的分布函数F(x),当$x=1$时,$F(1) = 1 - e^{-1}$。而当$x$接近1但小于1时,$F(x) = \frac{1}{2}$。因此,$P(X=1) = F(1) - \lim_{x \to 1^-} F(x) = (1 - e^{-1}) - \frac{1}{2} = \frac{1}{2} - e^{-1}$。