题目
1.15 试证: lim _(xarrow 0)dfrac ({R)_(e)z}(z) 不存在.
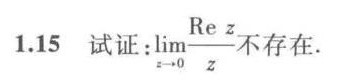
题目解答
答案

解析
考查要点:本题主要考查复变函数中复数极限的概念,以及如何通过不同路径趋近于某点来判断极限是否存在。
解题核心思路:在复变函数中,若沿不同路径趋近于某点时函数值趋于不同的结果,则该点的极限不存在。因此,构造不同的趋近路径,计算对应的极限值是否一致是关键。
破题关键点:
- 将复数表示为$x+yi$,将问题转化为实数表达式。
- 选择不同路径(如直线$y=kx$)趋近于$z=0$,观察极限是否随路径参数$k$变化而变化。
步骤1:设复数$z$的表达式
令$z = x + yi$(其中$x,y \in \mathbb{R}$),则$\text{Re}(z) = x$,原式变为:
$\frac{\text{Re}(z)}{z} = \frac{x}{x + yi}.$
步骤2:沿直线路径趋近于$z=0$
假设$z$沿直线$y = kx$趋近于$0$($k$为实数),则$z = x + kx i = x(1 + ki)$,代入得:
$\frac{x}{x(1 + ki)} = \frac{1}{1 + ki}.$
步骤3:分析极限值与$k$的关系
当$x \to 0$时,表达式$\frac{1}{1 + ki}$的值仅取决于$k$。例如:
- 若$k = 0$(沿实轴趋近),极限为$\frac{1}{1} = 1$;
- 若$k = 1$(沿直线$y = x$趋近),极限为$\frac{1}{1 + i} = \frac{1 - i}{2}$;
- 若$k = 2$(沿直线$y = 2x$趋近),极限为$\frac{1}{1 + 2i} = \frac{1 - 2i}{5}$。
结论:由于极限值随$k$变化而不同,原极限不存在。