题目
设随机变量sim U(1,6)，则sim U(1,6)（）A.对B.错
设随机变量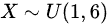
，则
（）
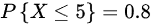A.对
B.错
题目解答
答案
已知随机变量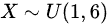，则密度函数
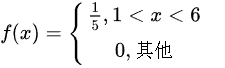，则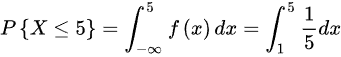
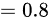，故选项是A。
解析
步骤 1：确定随机变量的分布
随机变量$X\sim U(1,6)$，表示$X$服从区间$(1,6)$上的均匀分布。均匀分布的密度函数为$f(x)=\frac{1}{b-a}$，其中$a$和$b$分别是区间的下限和上限。因此，对于$X\sim U(1,6)$，密度函数为$f(x)=\frac{1}{6-1}=\frac{1}{5}$，当$x$在$(1,6)$区间内时，否则$f(x)=0$。
步骤 2：计算概率$P\{ X\leqslant 5\}$
根据均匀分布的性质，$P\{ X\leqslant 5\}$可以通过计算密度函数在区间$(1,5)$上的积分得到。即$P\{ X\leqslant 5\} ={\int }_{-\infty }^{5}f(x)dx={\int }_{1}^{5}\frac{1}{5}dx$。由于$f(x)=\frac{1}{5}$在$(1,5)$区间内是常数，积分结果为$(5-1)\times\frac{1}{5}=4\times\frac{1}{5}=0.8$。
步骤 3：验证计算结果
根据步骤2的计算，$P\{ X\leqslant 5\} =0.8$，与题目中的条件一致，因此判断题目的说法是正确的。
随机变量$X\sim U(1,6)$，表示$X$服从区间$(1,6)$上的均匀分布。均匀分布的密度函数为$f(x)=\frac{1}{b-a}$，其中$a$和$b$分别是区间的下限和上限。因此，对于$X\sim U(1,6)$，密度函数为$f(x)=\frac{1}{6-1}=\frac{1}{5}$，当$x$在$(1,6)$区间内时，否则$f(x)=0$。
步骤 2：计算概率$P\{ X\leqslant 5\}$
根据均匀分布的性质，$P\{ X\leqslant 5\}$可以通过计算密度函数在区间$(1,5)$上的积分得到。即$P\{ X\leqslant 5\} ={\int }_{-\infty }^{5}f(x)dx={\int }_{1}^{5}\frac{1}{5}dx$。由于$f(x)=\frac{1}{5}$在$(1,5)$区间内是常数，积分结果为$(5-1)\times\frac{1}{5}=4\times\frac{1}{5}=0.8$。
步骤 3：验证计算结果
根据步骤2的计算，$P\{ X\leqslant 5\} =0.8$，与题目中的条件一致，因此判断题目的说法是正确的。