题目
写出下列随机试验的样本空间及下列事件包含的样本点:(1)掷一颗骰子,出现奇数点。(2)掷二颗骰子,A=“出现点数之和为奇数,且其中恰好有一个1点”,B="出现点数之和为偶数,但没有一颗骰子出现1点"。(3)将一枚硬币抛两次,A=“第一次出现正面”,B=“至少出现一次正面”,C=“两次出现同一面”。
写出下列随机试验的样本空间及下列事件包含的样本点:
(1)掷一颗骰子,出现奇数点。
(2)掷二颗骰子,A=“出现点数之和为奇数,且其中恰好有一个1点”,B="出现点数之和为偶数,但没有一颗骰子出现1点"。
(3)将一枚硬币抛两次,A=“第一次出现正面”,B=“至少出现一次正面”,C=“两次出现同一面”。
题目解答
答案
(1)掷一颗骰子的点数的样本空间为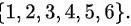
出现奇数点的样本点为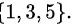
(2)掷二颗骰子的点数的样本空间为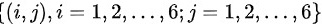 .
.
事件A等价于“出现的点数有1,另一个为偶数点”,因此,事件A的样本点为: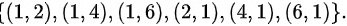
事件B的样本点为: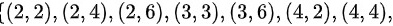
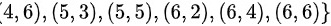
(3)将一枚硬币抛两次的样本空间为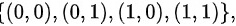 其中,0代表出现反面,1代表出现正面。
其中,0代表出现反面,1代表出现正面。
因此,事件A的样本点为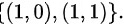
事件B等价于“出现一次正面或两次正面”,所以,其样本点为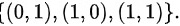
事件C等价于“同时出现正面或反面”,所以,其样本点为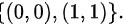
解析
样本空间是随机试验所有可能结果的集合,事件是样本空间中满足特定条件的子集。本题需分别分析三个试验的样本空间,并确定各事件对应的样本点:
- 单颗骰子的样本空间为$\{1,2,3,4,5,6\}$,奇数点事件直接筛选奇数。
- 两颗骰子的样本空间为有序对$(i,j)$,需结合点数之和奇偶性和是否含1点分析事件。
- 抛两次硬币的样本空间为$\{(0,0),(0,1),(1,0),(1,1)\}$,通过位置关系和出现次数确定事件样本点。
(1)掷一颗骰子
- 样本空间:$\{1,2,3,4,5,6\}$。
- 事件A(奇数点):筛选出奇数,即$\{1,3,5\}$。
(2)掷两颗骰子
- 样本空间:所有有序对$(i,j)$,其中$i,j \in \{1,2,3,4,5,6\}$。
- 事件A(和为奇数且恰好一个1点):
- 和为奇数要求一奇一偶。
- 恰好一个1点:若1点在奇数位置,则另一骰子为偶数(2,4,6)。
- 样本点:$\{(1,2),(1,4),(1,6),(2,1),(4,1),(6,1)\}$。
- 事件B(和为偶数且无1点):
- 和为偶数:两偶或两奇。
- 无1点:骰子点数只能是$\{2,3,4,5,6\}$。
- 两偶组合:$(2,2),(2,4),(2,6),(4,2),(4,4),(4,6),(6,2),(6,4),(6,6)$。
- 两奇组合:$(3,3),(3,5),(5,3),(5,5)$。
- 原答案错误:包含$(3,6)$(和为9,奇数,应排除),缺少$(3,5)$。
(3)抛两次硬币
- 样本空间:$\{(0,0),(0,1),(1,0),(1,1)\}$(0为反面,1为正面)。
- 事件A(第一次出现正面):第一次为1,即$\{(1,0),(1,1)\}$。
- 事件B(至少一次正面):排除$\{(0,0)\}$,即$\{(0,1),(1,0),(1,1)\}$。
- 事件C(两次同一面):$\{(0,0),(1,1)\}$。