题目
设 D 为平面区域^2+(y)^2leqslant 1 则 ^2+(y)^2leqslant 1 ?
设 D 为平面区域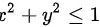 则
则 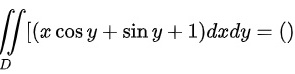 ?
?
题目解答
答案
解:
将函数分为三个部分
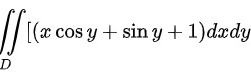
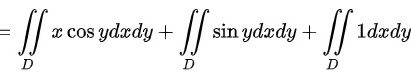
对第一部分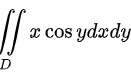
已知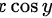 是关于
是关于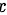 的奇函数,且定义域关于
的奇函数,且定义域关于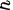 轴对称
轴对称
因此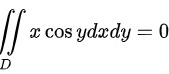
对第二部分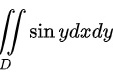
已知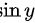 是关于
是关于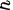 的奇函数,且定义域关于
的奇函数,且定义域关于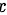 轴对称
轴对称
因此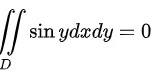
对第三部分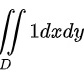
令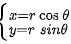 ,有
,有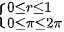
有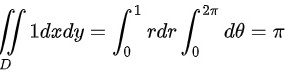
即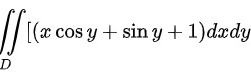
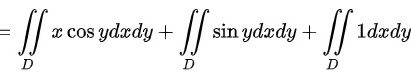
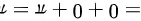
综上所述,

解析
步骤 1:将函数分为三个部分
将给定的积分函数分为三个部分,分别计算每个部分的积分。
步骤 2:计算第一部分的积分
第一部分为$x\cos y$,由于$x\cos y$关于$x$是奇函数,且定义域关于$x$轴对称,因此这部分的积分结果为0。
步骤 3:计算第二部分的积分
第二部分为$\sin y$,由于$\sin y$关于$x$是奇函数,且定义域关于$x$轴对称,因此这部分的积分结果为0。
步骤 4:计算第三部分的积分
第三部分为1,这部分的积分结果为区域D的面积。由于D为单位圆,其面积为$\pi$。
步骤 5:将三部分的积分结果相加
将三部分的积分结果相加,得到最终的积分结果。
将给定的积分函数分为三个部分,分别计算每个部分的积分。
步骤 2:计算第一部分的积分
第一部分为$x\cos y$,由于$x\cos y$关于$x$是奇函数,且定义域关于$x$轴对称,因此这部分的积分结果为0。
步骤 3:计算第二部分的积分
第二部分为$\sin y$,由于$\sin y$关于$x$是奇函数,且定义域关于$x$轴对称,因此这部分的积分结果为0。
步骤 4:计算第三部分的积分
第三部分为1,这部分的积分结果为区域D的面积。由于D为单位圆,其面积为$\pi$。
步骤 5:将三部分的积分结果相加
将三部分的积分结果相加,得到最终的积分结果。