题目
将根式化为指数分数形式: dfrac (1)(sqrt {1+{x)^2}}

题目解答
答案
要将 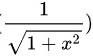 化为指数分数形式,我们可以利用公式:
化为指数分数形式,我们可以利用公式:
[
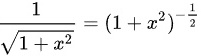
]
这里 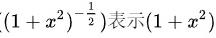 的幂指数为 (-
的幂指数为 (-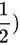 ,即其倒数的平方根
,即其倒数的平方根
解析
考查要点:本题主要考查根式与指数形式的相互转换,需要掌握根式转化为分数指数幂的基本规则,以及负指数表示倒数的概念。
解题核心思路:
- 根式转指数:将根号$\sqrt{A}$表示为$A^{\frac{1}{2}}$。
- 倒数转负指数:将分母中的表达式转化为分子的负指数形式,即$\frac{1}{A} = A^{-1}$。
- 综合应用:结合上述两步,将$\frac{1}{\sqrt{1+x^2}}$逐步改写为指数形式。
破题关键点:
- 明确根式与分数指数的对应关系,注意运算顺序(先开根号,再取倒数)。
- 正确应用负指数规则,将分母的表达式转换为分子的负指数形式。
步骤1:处理根号
原式中的分母$\sqrt{1+x^2}$可以表示为分数指数形式:
$\sqrt{1+x^2} = (1+x^2)^{\frac{1}{2}}$
步骤2:处理倒数
将原式$\frac{1}{\sqrt{1+x^2}}$改写为:
$\frac{1}{(1+x^2)^{\frac{1}{2}}} = (1+x^2)^{-\frac{1}{2}}$
关键结论:
通过将根号转换为分数指数,再利用负指数表示倒数,最终得到指数分数形式。