题目
7.求函数 =dfrac (1-x)(1+2x) 的反函数.
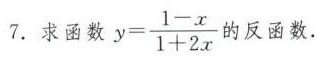
题目解答
答案

解析
步骤 1:交换变量
将原函数中的 $x$ 和 $y$ 互换,得到 $x=\dfrac {1-y}{1+2y}$。
步骤 2:解方程
解方程 $x=\dfrac {1-y}{1+2y}$,以 $y$ 为未知数。
步骤 3:整理方程
将方程 $x=\dfrac {1-y}{1+2y}$ 两边同时乘以 $(1+2y)$,得到 $x(1+2y)=1-y$。
步骤 4:移项
将方程 $x(1+2y)=1-y$ 移项,得到 $x+2xy=1-y$。
步骤 5:整理方程
将方程 $x+2xy=1-y$ 整理为 $2xy+y=1-x$。
步骤 6:提取公因式
将方程 $2xy+y=1-x$ 提取公因式 $y$,得到 $y(2x+1)=1-x$。
步骤 7:解出 $y$
将方程 $y(2x+1)=1-x$ 解出 $y$,得到 $y=\dfrac {1-x}{2x+1}$。
将原函数中的 $x$ 和 $y$ 互换,得到 $x=\dfrac {1-y}{1+2y}$。
步骤 2:解方程
解方程 $x=\dfrac {1-y}{1+2y}$,以 $y$ 为未知数。
步骤 3:整理方程
将方程 $x=\dfrac {1-y}{1+2y}$ 两边同时乘以 $(1+2y)$,得到 $x(1+2y)=1-y$。
步骤 4:移项
将方程 $x(1+2y)=1-y$ 移项,得到 $x+2xy=1-y$。
步骤 5:整理方程
将方程 $x+2xy=1-y$ 整理为 $2xy+y=1-x$。
步骤 6:提取公因式
将方程 $2xy+y=1-x$ 提取公因式 $y$,得到 $y(2x+1)=1-x$。
步骤 7:解出 $y$
将方程 $y(2x+1)=1-x$ 解出 $y$,得到 $y=\dfrac {1-x}{2x+1}$。