题目
下列陈述中,哪些是对的,哪些是错的?如果是对的,说明理由;如果是-|||-错的,试给出一个反例.-|||-(1)如果函数f(x)在a连续,那么|f (x)|也在a连续;-|||-(2)如果函数|f(x)|在a连续,那么f(x)也在a连续.

题目解答
答案
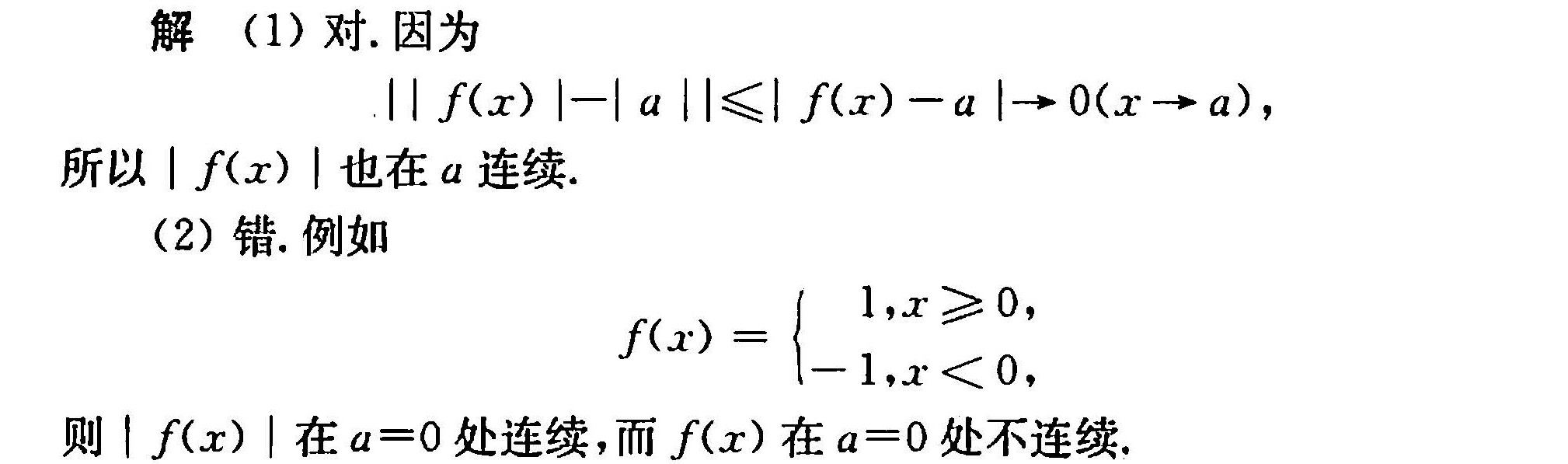
解析
考查要点:本题主要考查函数连续性的性质,特别是绝对值函数对连续性的影响。需要理解连续函数的定义及绝对值运算对函数连续性的影响关系。
解题核心思路:
- 绝对值函数的连续性:若原函数连续,其绝对值函数必然连续,可通过三角不等式证明。
- 逆命题的反例构造:绝对值函数连续时,原函数不一定连续,需构造反例说明。
破题关键点:
- 直接应用连续性定义:通过比较$|f(x)|$与$f(x)$的极限关系判断连续性。
- 反例构造技巧:寻找在某点处绝对值函数平滑但原函数存在跳跃或可去不连续点的例子。
第(1)题
判断:正确。
理由:
根据连续函数的定义,若$f(x)$在$a$处连续,则$\lim\limits_{x \to a} f(x) = f(a)$。
考虑$|f(x)|$的连续性,利用三角不等式:
$\left| |f(x)| - |f(a)| \right| \leq |f(x) - f(a)|.$
当$x \to a$时,右侧$|f(x) - f(a)| \to 0$,因此左侧$\left| |f(x)| - |f(a)| \right| \to 0$,即$\lim\limits_{x \to a} |f(x)| = |f(a)|$,故$|f(x)|$在$a$处连续。
第(2)题
判断:错误。
反例:
构造函数
$f(x) =
\begin{cases} 1, & x \geq 0, \\-1, & x < 0.\end{cases}$
- 分析$|f(x)|$的连续性:
$|f(x)| = 1$对所有$x$成立,显然在$a=0$处连续。 - 分析$f(x)$的连续性:
当$x \to 0^+$时,$\lim f(x) = 1$;当$x \to 0^-$时,$\lim f(x) = -1$,左右极限不相等,故$f(x)$在$a=0$处不连续。