题目
20.口袋中有一个球,不知它的颜色是黑的还是白的.现再往口袋中放入一个白球,然后从口袋中任意取出一个,发现取出的是白球,试问口袋中原来那个球是白球的可能性为多少?
20.口袋中有一个球,不知它的颜色是黑的还是白的.现再往口袋中放入一个白球,然后从口袋中任意取出一个,发现取出的是白球,试问口袋中原来那个球是白球的可能性为多少?
题目解答
答案
口袋中原来那个球是白球的可能性为 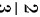
根据题目描述,口袋中最开始有一个球,有两种可能情况,即黑球或白球,因此先验概率分别为 P(C=B) = 0.5 和 P(C=W) = 0.5,其中 C表示原来口袋中的球的颜色,B表示黑球,W表示白球。
现在往口袋中放入一个白球,变成了包含一个黑球和两个白球的口袋。现在从口袋中任意取一球,发现取出的是一个白球,需要计算在这个条件下口袋中原来的球是白球的后验概率,即:
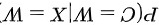
其中 X=W 表示从口袋中取出的球是白球。
根据贝叶斯公式,有:
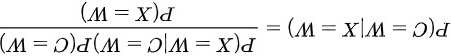
需要分别计算分子和分母。
先计算分子,有:
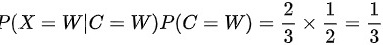
其中,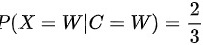 表示在口袋中原来是白球的情况下,从中取出一个白球的概率(因为现在口袋中一共有两个白球和一个黑球),
表示在口袋中原来是白球的情况下,从中取出一个白球的概率(因为现在口袋中一共有两个白球和一个黑球),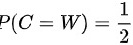 表示先验概率。
表示先验概率。
再计算分母,有:
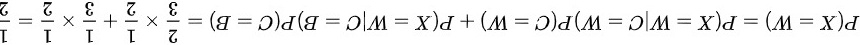
其中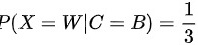 表示在口袋中原来是黑球的情况下,从中取出一个白球的概率。
表示在口袋中原来是黑球的情况下,从中取出一个白球的概率。
因此,代入贝叶斯公式得到:
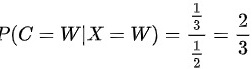
因此,口袋中原来那个球是白球的可能性为 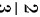
解析
考查要点:本题主要考查条件概率和贝叶斯定理的应用,需要根据已知结果反推初始状态的概率。
解题核心思路:
- 明确初始状态:口袋中最初有一个球,颜色可能是黑或白,先验概率均为$\frac{1}{2}$。
- 构建可能情况:放入一个白球后,口袋中总共有两个球,需分别考虑原来球为黑或白时的取球概率。
- 应用贝叶斯定理:通过条件概率公式计算后验概率,即取出白球时原来球为白球的概率。
破题关键点:
- 正确计算条件概率:当原来球为白时,口袋中有两个白球,取白球的概率为$1$;当原来球为黑时,口袋中有一个白球和一个黑球,取白球的概率为$\frac{1}{2}$。
- 区分分子与分母:分子对应原来球为白且取出白球的联合概率,分母对应所有可能情况下取出白球的总概率。
步骤1:定义事件与先验概率
- 设$C=W$表示原来球为白,$C=B$表示原来球为黑,先验概率均为$\frac{1}{2}$。
- 取出白球的事件记为$X=W$。
步骤2:计算条件概率
- 若原来球为白:口袋中有两个白球,取白球的概率为$P(X=W|C=W)=1$。
- 若原来球为黑:口袋中有一个白球和一个黑球,取白球的概率为$P(X=W|C=B)=\frac{1}{2}$。
步骤3:应用贝叶斯定理
后验概率公式为:
$P(C=W|X=W) = \frac{P(X=W|C=W) \cdot P(C=W)}{P(X=W)}$
- 分子:$P(X=W|C=W) \cdot P(C=W) = 1 \cdot \frac{1}{2} = \frac{1}{2}$。
- 分母:$P(X=W) = P(X=W|C=W) \cdot P(C=W) + P(X=W|C=B) \cdot P(C=B) = 1 \cdot \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{2} = \frac{3}{4}$。
- 代入公式:
$P(C=W|X=W) = \frac{\frac{1}{2}}{\frac{3}{4}} = \frac{2}{3}$