题目
10. lim _(xarrow 0)sqrt [n](1+x)= 1
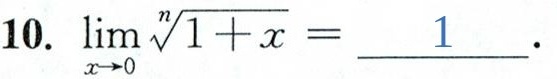
题目解答
答案
答案见上
解析
考查要点:本题主要考查极限的基本性质以及连续函数的运算规则。关键在于理解根号函数在特定点的连续性,从而简化极限计算。
解题核心思路:
当$x \to 0$时,$1+x$趋近于$1$,而n次根号函数在$1$处连续。因此,极限运算可以与根号运算交换顺序,直接代入$x=0$即可得到结果。
破题关键点:
- 明确根号函数$\sqrt[n]{\cdot}$在$1$处的连续性。
- 应用极限的运算规则,将极限符号移到根号外。
步骤1:分析函数连续性
n次根号函数$f(y) = \sqrt[n]{y}$在$y=1$处连续,因此:
$\lim_{y \to 1} \sqrt[n]{y} = \sqrt[n]{\lim_{y \to 1} y} = \sqrt[n]{1} = 1.$
步骤2:代入原极限表达式
在原题中,当$x \to 0$时,$1+x \to 1$,因此:
$\lim_{x \to 0} \sqrt[n]{1+x} = \sqrt[n]{\lim_{x \to 0} (1+x)} = \sqrt[n]{1} = 1.$