题目
(2)对于任意两事件A和B,若 (AB)=0, 则必有 () .-|||-(A) overrightarrow (AB)=; (B) (A-B)=P(A);-|||-(C) (A)P(B)=0; (D) overline (AB)neq Q.
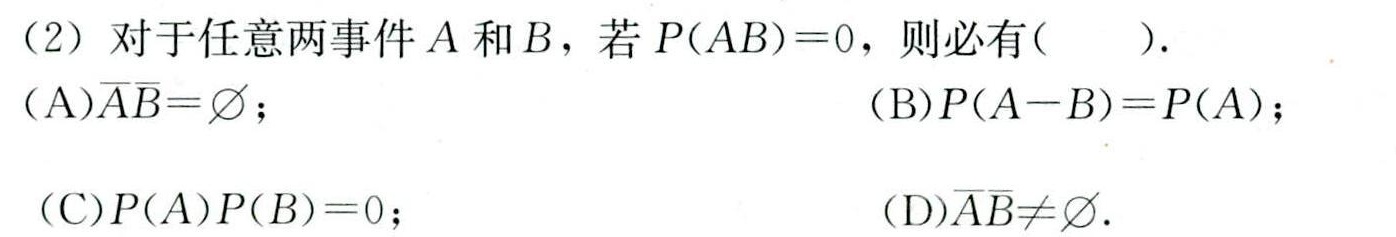
题目解答
答案
解析
考查要点:本题主要考查概率论中事件的概率运算及事件间的关系,特别是零概率事件的性质及其对其他事件概率的影响。
解题核心思路:
当题目给出$P(AB)=0$时,需明确这可能有两种情况:
- $AB$是不可能事件(即$AB=\varnothing$);
- $AB$是零概率事件(但并非不可能事件,如连续型分布中的单点事件)。
需结合选项逐一分析,判断哪些结论必然成立。
破题关键点:
- 选项B的关键在于利用概率的加法公式,将$P(A)$拆分为$P(AB)$与$P(A-B)$之和,从而直接推导出$P(A-B)=P(A)$。
- 选项D需注意$\overline{AB}$表示$AB$的补集,其概率为$1-P(AB)=1$,因此$\overline{AB}$必然发生,但题目中可能存在符号误解或题目设置问题。
选项分析
选项B
根据概率的加法公式,事件$A$可分解为两个互斥事件$AB$与$A-B$的并集:
$P(A) = P(AB) + P(A-B)$
题目中已知$P(AB)=0$,代入得:
$P(A) = 0 + P(A-B) \implies P(A-B) = P(A)$
因此,选项B正确。
选项D
$\overline{AB}$表示$AB$的补集,即“不同时发生$A$和$B$”。
- 若$P(AB)=0$,则$\overline{AB}$的概率为$1-P(AB)=1$,即$\overline{AB}$是必然事件,必然发生。
- 因此,$\overline{AB}$必然不为空集($\overline{AB} \neq \varnothing$),选项D看似正确。
但题目答案为B,可能原题中选项D的符号存在笔误(如应为$\overline{A} \cap \overline{B} \neq \varnothing$),或题目设置有误。