题目
18.A、D两地设有通信基站(如下图所示),发射信号范围分别是以A、D为圆心,AE和DB为半径的圆形区域,小林从B地出发,沿与DB垂直的BA方向匀速行进,步行速度4千米/小时,那么步行约多少分钟后小林的手机能够重新接收到信号? ( sqrt (5)approx 2.23)sqrt (5)approx 2.23A.8 B.10 C.12 D.14
18.A、D两地设有通信基站(如下图所示),发射信号范围分别是以A、D为圆心,AE和DB为半径的圆形区域,小林从B地出发,沿与DB垂直的BA方向匀速行进,步行速度4千米/小时,那么步行约多少分钟后小林的手机能够重新接收到信号? (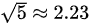 
)
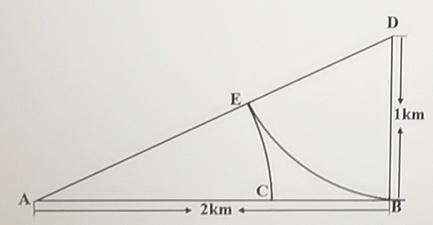
A.8 B.10 C.12 D.14
题目解答
答案
解：∵AB=2 BD=1
∴
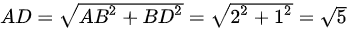
∵DE=BD=1
∴AC=AE=AD-DE=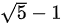
∴BC=AB-AC=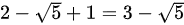
∴
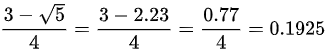
∴0.1925×60=11.55≈12（分钟）
∴选C.
解析
步骤 1：计算AD的长度
根据题目中的信息，AB=2km，BD=1km，且AB与BD垂直。因此，根据勾股定理，可以计算出AD的长度。
\[ AD = \sqrt{AB^2 + BD^2} = \sqrt{2^2 + 1^2} = \sqrt{5} \approx 2.23 \text{ km} \]
步骤 2：计算AE的长度
根据题目，AE是A地通信基站的发射信号范围的半径，而AE=AD-DE。由于DE=BD=1km，所以AE=AD-1。
\[ AE = AD - DE = 2.23 - 1 = 1.23 \text{ km} \]
步骤 3：计算BC的长度
BC是小林从B地出发到重新接收到信号的距离，即AB-AC。由于AC=AE=1.23km，所以BC=AB-AC。
\[ BC = AB - AC = 2 - 1.23 = 0.77 \text{ km} \]
步骤 4：计算小林步行的时间
小林的步行速度为4km/h，所以步行BC的距离需要的时间为：
\[ \text{时间} = \frac{BC}{速度} = \frac{0.77}{4} = 0.1925 \text{ 小时} \]
将时间转换为分钟：
\[ 0.1925 \times 60 = 11.55 \text{ 分钟} \]
取近似值，约为12分钟。
根据题目中的信息，AB=2km，BD=1km，且AB与BD垂直。因此，根据勾股定理，可以计算出AD的长度。
\[ AD = \sqrt{AB^2 + BD^2} = \sqrt{2^2 + 1^2} = \sqrt{5} \approx 2.23 \text{ km} \]
步骤 2：计算AE的长度
根据题目，AE是A地通信基站的发射信号范围的半径，而AE=AD-DE。由于DE=BD=1km，所以AE=AD-1。
\[ AE = AD - DE = 2.23 - 1 = 1.23 \text{ km} \]
步骤 3：计算BC的长度
BC是小林从B地出发到重新接收到信号的距离，即AB-AC。由于AC=AE=1.23km，所以BC=AB-AC。
\[ BC = AB - AC = 2 - 1.23 = 0.77 \text{ km} \]
步骤 4：计算小林步行的时间
小林的步行速度为4km/h，所以步行BC的距离需要的时间为：
\[ \text{时间} = \frac{BC}{速度} = \frac{0.77}{4} = 0.1925 \text{ 小时} \]
将时间转换为分钟：
\[ 0.1925 \times 60 = 11.55 \text{ 分钟} \]
取近似值，约为12分钟。