题目
求曲线^dfrac (2{3)}+(y)^dfrac (2{3)}=(a)^dfrac (2{3)},在点^dfrac (2{3)}+(y)^dfrac (2{3)}=(a)^dfrac (2{3)}处的切线方程和法线方程。
求曲线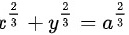 ,在点
,在点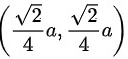 处的切线方程和法线方程。
处的切线方程和法线方程。
题目解答
答案
对曲线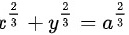 方程两边同时微分得到:
方程两边同时微分得到: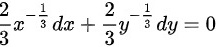 故而得到:
故而得到: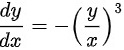 ,故而可以求出点
,故而可以求出点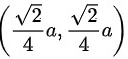 处的切线方程的斜率为:
处的切线方程的斜率为: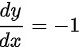 ,故而法线方程的斜率为:
,故而法线方程的斜率为: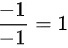 .故而切线方程为:
.故而切线方程为: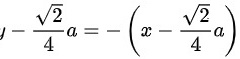 即:
即: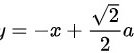 .法线方程为:
.法线方程为: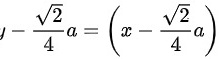 ,即:
,即: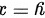
综上本题答案为:曲线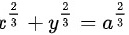 ,在点
,在点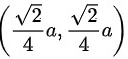 处的切线方程为
处的切线方程为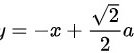 ,法线方程为
,法线方程为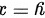
解析
步骤 1:隐函数求导
对曲线${c}^{\dfrac {2}{3}}+{y}^{\dfrac {2}{3}}={a}^{\dfrac {2}{3}}$方程两边同时微分得到:$\dfrac {2}{3}{x}^{-\dfrac {1}{3}}dx+\dfrac {2}{3}{y}^{-\dfrac {1}{3}}dy=0$,从而得到$\dfrac {dy}{dx}=-{(\dfrac {y}{x})}^{3}$。
步骤 2:计算切线斜率
将点$(\dfrac {\sqrt {2}}{4}a,\dfrac {\sqrt {2}}{4}a)$代入$\dfrac {dy}{dx}=-{(\dfrac {y}{x})}^{3}$,得到切线斜率为$-1$。
步骤 3:计算法线斜率
由于切线斜率为$-1$,则法线斜率为$1$(因为切线斜率与法线斜率互为负倒数)。
步骤 4:求切线方程
利用点斜式方程$y-y_1=m(x-x_1)$,其中$m$为斜率,$(x_1,y_1)$为点$(\dfrac {\sqrt {2}}{4}a,\dfrac {\sqrt {2}}{4}a)$,代入得到切线方程$y=-x+\dfrac {\sqrt {2}}{2}a$。
步骤 5:求法线方程
同样利用点斜式方程$y-y_1=m(x-x_1)$,其中$m$为斜率,$(x_1,y_1)$为点$(\dfrac {\sqrt {2}}{4}a,\dfrac {\sqrt {2}}{4}a)$,代入得到法线方程$y=x-\dfrac {\sqrt {2}}{2}a+\dfrac {\sqrt {2}}{4}a$,简化后得到$y=x-\dfrac {\sqrt {2}}{4}a$。
对曲线${c}^{\dfrac {2}{3}}+{y}^{\dfrac {2}{3}}={a}^{\dfrac {2}{3}}$方程两边同时微分得到:$\dfrac {2}{3}{x}^{-\dfrac {1}{3}}dx+\dfrac {2}{3}{y}^{-\dfrac {1}{3}}dy=0$,从而得到$\dfrac {dy}{dx}=-{(\dfrac {y}{x})}^{3}$。
步骤 2:计算切线斜率
将点$(\dfrac {\sqrt {2}}{4}a,\dfrac {\sqrt {2}}{4}a)$代入$\dfrac {dy}{dx}=-{(\dfrac {y}{x})}^{3}$,得到切线斜率为$-1$。
步骤 3:计算法线斜率
由于切线斜率为$-1$,则法线斜率为$1$(因为切线斜率与法线斜率互为负倒数)。
步骤 4:求切线方程
利用点斜式方程$y-y_1=m(x-x_1)$,其中$m$为斜率,$(x_1,y_1)$为点$(\dfrac {\sqrt {2}}{4}a,\dfrac {\sqrt {2}}{4}a)$,代入得到切线方程$y=-x+\dfrac {\sqrt {2}}{2}a$。
步骤 5:求法线方程
同样利用点斜式方程$y-y_1=m(x-x_1)$,其中$m$为斜率,$(x_1,y_1)$为点$(\dfrac {\sqrt {2}}{4}a,\dfrac {\sqrt {2}}{4}a)$,代入得到法线方程$y=x-\dfrac {\sqrt {2}}{2}a+\dfrac {\sqrt {2}}{4}a$,简化后得到$y=x-\dfrac {\sqrt {2}}{4}a$。