(1)给出事件A、B的例子,使得(i)P(A B)<P(A),(ii)P(A B)=P(A) (iii)P(A B)>P(A)(2)设事件A、B、C相互独立,证明:(i)C与AB相互独立 (ii)C与AB相互独立。(3)设事件A的概率P(A)=0,证明对于任意另一事件B,有A、B相互独立。(4)证明事件A、B相互独立的充要条件是P(A B)=P(A B)
题目解答
答案
答:(1)(i)当事件B发生会是事件A发生的概率减小时,P(A B)<P(A)
比如A是骑自行车上学的学生,B是男生,全集是所有学生
(ii)当事件B发生对A没有影响,即A、B互为独立事件时,P(A B)=P(A)
比如事件A是扔骰子得到一点,事件B是明天下雨。
(iii)当事件B发生会是事件A发生的概率增加时,P(A B)>P(A)
比如事件A是课余时间我去健身,事件B是课余时间室友们健身,显然他们很有可能对我的决定产生影响。
(2)(i)∵A、B、C相互独立
∴P(ABC)=P(A)P(B)P(C)=P(AB)P(C)
即P((AB)C)=P(AB)P(C) ∴C与AB相互独立
(ii)P(A∪B)=P(A)+P(B)-P(AB)
∴P(A∪B)P(C)=P(A)P(C)+P(B)P(C)-P(AB)P(C)=P((A∪B)C)
∴C与A∪B相互独立
(3)因ABA,故若P(A)=0,则
0≪P(AB)≪P(A)
从而 P(AB)=0=P(B)∙0=P(B)∙P(A)
按定义,A,B相互独立。
(4)必要性.设A,B相互独立,则A, 也相互独立,从而只P(A|B)=P(A), P(A|)=P(A).故P(A|B)= P(A|).
充分性.设P(A|B)= P(A|),按定义此式即表示
=
由比例的性质得
 =
=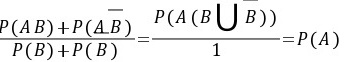
解析
题目(1):事件概率关系举例
考察对事件交集概率与事件概率大小关系的理解,核心是事件间的影响方向:
- (i) $P(AB) < P(A)$:需$B$发生降低$A$发生的可能性,即$B$对$A$有负影响。例如“$A$为骑自行车上学的学生,$B$为男生”,因男生可能更多选择其他交通工具,导致$AB$概率小于$A$。
- (ii) $P(AB) = P(A)$:需$B$对$A$无影响,即$A$与$B$独立($P(AB)=P(A)P(B)$,若$P(B)≠0$则$P(A)=P(AB)$)。例如“$A$为扔骰子得1点,$B$为明天下雨”,两者无关,交集概率等于$A$的概率。
- (iii) $P(AB) > P(A)$:需$B$发生提高$A$发生的可能性,即$B$对$A$有正影响。例如“$A$为课余健身,$B$为室友课余健身”,室友健身可能带动自己健身,交集概率大于$A$。
题目(2):相互独立事件的性质
考察事件相互独立的定义($P(ABC)=P(A)P(B)P(C)$及$P(AC)=P(A)P(C)$等):
- (i) $C$与$AB$独立:
因$A,B,C$相互独立,故$P(ABC)=P(A)P(B)P(C)=P(AB)P(C)$,即$P((AB)C)=P(AB)P(C)$,由独立性定义得$C$与$AB$独立。 - (ii) $C$与$A∪B$独立:
先展开$P((A∪B)C)=P(AC∪BC)=P(AC)+P(BC)-P(ABC)$,代入独立性:
$P(AC)+P(BC)-P(ABC)=P(A)P(C)+P(B)P(C)-P(A)P(B)P(C)=P(C)[P(A)+P(B)-P(AB)]=P(C)P(A∪B)$,故$C$与$A∪B$独立。
题目(3):概率为0的事件与任意事件独立
考察独立性定义($P(AB)=P(A)P(B)$):
因$AB⊆A$,故$P(AB)≤P(A)=0$,又概率非负,得$P(AB)=0$。对任意$B$,$P(A)P(B)=0×P(B)=0=P(AB)$,满足独立性定义,故$A,B$独立。
题目(4):$A,B$独立的充要条件
考察条件概率与独立性的等价性:
- 必要性:若$A,B$独立,则$P(A|B)=P(A)$且$P(A|\overline{B})=P(A)$(独立事件的条件概率等于边际概率),故$P(A|B)=P(A|\overline{B})$。
- 充分性:若$P(A|B)=P(A|\overline{B})$,则$\frac{P(AB)}{P(B)}=\frac{P(A\overline{B})}{P(\overline{B})}$,交叉相乘得$P(AB)P(\overline{B})=P(A\overline{B})P(B)$。展开$P(\overline{B})=1-P(B)$,$P(A\overline{B})=P(A)-P(AB)$,代入化简得$P(AB)=P(A)P(B)$,即$A,B$独立。