题目
int dfrac ({x)^2}({x)^2+1}dx ,
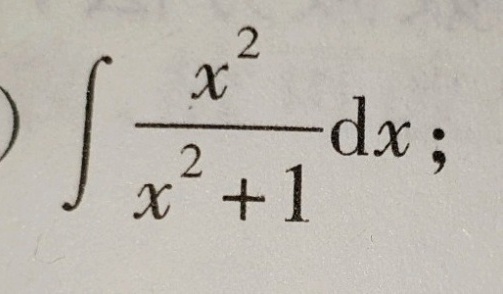
题目解答
答案
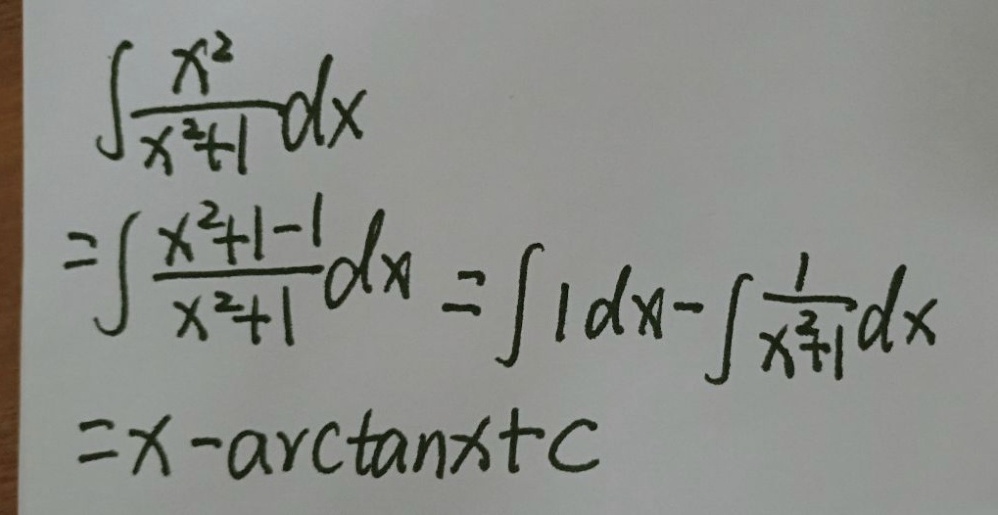
解析
步骤 1:分解被积函数
将被积函数 $\dfrac{{x}^{2}}{{x}^{2}+1}$ 分解为两个部分,以便于积分。注意到 ${x}^{2}+1$ 可以写成 ${x}^{2}+1-1+1$,这样可以将被积函数写成 $\dfrac{{x}^{2}+1-1}{{x}^{2}+1}$。
步骤 2:简化被积函数
将被积函数 $\dfrac{{x}^{2}+1-1}{{x}^{2}+1}$ 分解为 $\dfrac{{x}^{2}+1}{{x}^{2}+1}-\dfrac{1}{{x}^{2}+1}$,即 $1-\dfrac{1}{{x}^{2}+1}$。
步骤 3:积分
对简化后的被积函数进行积分,即 $\int 1dx-\int \dfrac{1}{{x}^{2}+1}dx$。其中,$\int 1dx$ 的结果是 $x$,而 $\int \dfrac{1}{{x}^{2}+1}dx$ 的结果是 $\arctan x$。
将被积函数 $\dfrac{{x}^{2}}{{x}^{2}+1}$ 分解为两个部分,以便于积分。注意到 ${x}^{2}+1$ 可以写成 ${x}^{2}+1-1+1$,这样可以将被积函数写成 $\dfrac{{x}^{2}+1-1}{{x}^{2}+1}$。
步骤 2:简化被积函数
将被积函数 $\dfrac{{x}^{2}+1-1}{{x}^{2}+1}$ 分解为 $\dfrac{{x}^{2}+1}{{x}^{2}+1}-\dfrac{1}{{x}^{2}+1}$,即 $1-\dfrac{1}{{x}^{2}+1}$。
步骤 3:积分
对简化后的被积函数进行积分,即 $\int 1dx-\int \dfrac{1}{{x}^{2}+1}dx$。其中,$\int 1dx$ 的结果是 $x$,而 $\int \dfrac{1}{{x}^{2}+1}dx$ 的结果是 $\arctan x$。