题目
一口袋中有3个红球和2个白球,某人从该口袋中随机摸出一球,摸得红球得5分,摸得白球得2分,则他所得分数的数学期望为( )A. 2.5 B. 3.5 C. 3.8 D. 以上都不对
一口袋中有3个红球和2个白球,某人从该口袋中随机摸出一球,摸得红球得5分,摸得白球得2分,则他所得分数的数学期望为( )
A. 2.5B. 3.5
C. 3.8
D. 以上都不对
题目解答
答案
选C, 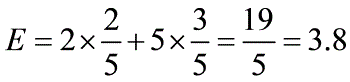
解析
步骤 1:确定随机变量的取值
设随机变量X表示摸球所得的分数,根据题意,X的取值为5(摸得红球)和2(摸得白球)。
步骤 2:计算随机变量取值的概率
摸得红球的概率为P(X=5) = 3/5,摸得白球的概率为P(X=2) = 2/5。
步骤 3:计算数学期望
数学期望E(X) = Σ[xi * P(X=xi)],其中xi为随机变量X的取值,P(X=xi)为随机变量X取值xi的概率。
E(X) = 5 * (3/5) + 2 * (2/5) = 15/5 + 4/5 = 19/5 = 3.8。
设随机变量X表示摸球所得的分数,根据题意,X的取值为5(摸得红球)和2(摸得白球)。
步骤 2:计算随机变量取值的概率
摸得红球的概率为P(X=5) = 3/5,摸得白球的概率为P(X=2) = 2/5。
步骤 3:计算数学期望
数学期望E(X) = Σ[xi * P(X=xi)],其中xi为随机变量X的取值,P(X=xi)为随机变量X取值xi的概率。
E(X) = 5 * (3/5) + 2 * (2/5) = 15/5 + 4/5 = 19/5 = 3.8。