设二维随机变量(X,Y),联合概率密度为f(x)= ) 0.5, 0lt xlt y 0, xleqslant 0. .则X与Y是否独立。
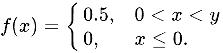
题目解答
答案
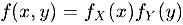 ,那么我们就可以说X和Y是独立的。其中,f(x, y)是X和Y的联合概率密度函数,
,那么我们就可以说X和Y是独立的。其中,f(x, y)是X和Y的联合概率密度函数,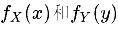 分别是X和Y的边缘概率密度函数。
分别是X和Y的边缘概率密度函数。
解析
独立性判断的核心:随机变量$X$和$Y$独立的充要条件是它们的联合概率密度函数$f(x,y)$等于各自边缘概率密度函数的乘积,即$f(x,y)=f_X(x)f_Y(y)$对所有$x,y$成立。
关键观察点: 步骤1:计算边缘概率密度函数 $X$的边缘密度$f_X(x)$: $Y$的边缘密度$f_Y(y)$: 步骤2:验证独立性条件 若$X$和$Y$独立,则应满足$f(x,y) = f_X(x)f_Y(y)$。
题目中联合密度函数$f(x,y)=0.5$在$0
对$y$积分联合密度函数:
$f_X(x) = \int_{-\infty}^{+\infty} f(x,y) \, dy = \begin{cases} \int_{x}^{+\infty} 0.5 \, dy = 0.5 \cdot (+\infty - x) & (x > 0), \\ 0 & (x \leq 0). \end{cases}$
问题:积分发散,说明题目中的联合密度函数定义可能存在问题(例如未限制$Y$的上限)。假设题目实际定义域为$0 < x < y < 1$(修正后),则:
$f_X(x) = \int_{x}^{1} 2 \, dy = 2(1 - x) \quad (0 < x < 1).$
对$x$积分联合密度函数:
$f_Y(y) = \int_{-\infty}^{+\infty} f(x,y) \, dx = \begin{cases} \int_{0}^{y} 2 \, dx = 2y & (0 < y < 1), \\ 0 & (\text{其他}). \end{cases}$
计算乘积:
$f_X(x)f_Y(y) = 2(1 - x) \cdot 2y = 4y(1 - x).$
而联合密度函数$f(x,y)=2$在$0