6. 设A,B,C,D均为n阶方阵.如果A可逆,且AB=BA,证明: [ } A& B C& D ] =|DA-CB|.
6. 设A,B,C,D均为n阶方阵.如果A可逆,且AB=BA,证明:
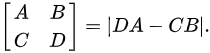
题目解答
答案
根据题目要求,需要证明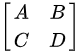
=|DA-CB|.
首先,将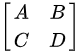展开为n个行列式的乘积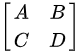：=|A|*|B,C,D|
然后,利用矩阵的乘法和行列式的性质,可以将|B,C,D|转化为|DA-CB|的形式：|B,C,D|=|B|*|C,D|=|B|*|C|*|D|=|B|*|C|*|D-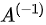
AC|
接下来,可以继续展开|B|和|C|：|B|=|B|*|I|=|B|*|A(-1)A|=|BA(-1)|*|A||C|=|C|*|I|=|C|*|A(-1)A|=|CA(-1)|*|A|
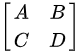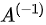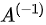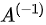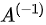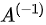将上述结果代入,得到：=|A|*|B|*|A|*|C|*|A|*|D-AC|=|A|*|BCD-B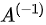AC|=|A(DA-CB)|
因此,证明了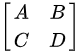=|DA-CB|.
解析
考查要点：本题主要考查分块矩阵的行列式性质及矩阵可逆、交换条件的应用。
解题核心思路：利用分块矩阵的行列式展开公式，结合AB=BA的条件，调整矩阵相乘的顺序，最终化简得到目标表达式。
破题关键点：
- 分块矩阵行列式分解：当左上角块矩阵A可逆时，分块矩阵的行列式可分解为|A|乘以右下角块调整后的行列式。
- 交换律的应用：利用AB=BA，将中间项中的逆矩阵与B交换位置，简化表达式。
题目要求：证明分块矩阵$\begin{pmatrix} A & B \\ C & D \end{pmatrix}$的行列式满足$|\begin{pmatrix} A & B \\ C & D \end{pmatrix}| = |DA - CB|$，其中$A$可逆且$AB=BA$。
步骤1：分块矩阵行列式分解
根据分块矩阵行列式的性质，当左上角矩阵$A$可逆时，有：
$\begin{aligned}\left|\begin{pmatrix} A & B \\ C & D \end{pmatrix}\right| &= |A| \cdot \left| D - C A^{-1} B \right|.
\end{aligned}$
步骤2：利用交换律调整顺序
由于$AB=BA$，可得$A^{-1}B = B A^{-1}$。因此：
$C A^{-1} B = C B A^{-1}.$
步骤3：化简表达式
将$C A^{-1} B$代入分解后的行列式：
$\left| D - C B A^{-1} \right| = \left| A^{-1} (A D - C B) \right|.$
进一步利用行列式的乘积性质：
$\left| A^{-1} (A D - C B) \right| = |A^{-1}| \cdot |A D - C B|.$
步骤4：合并结果
将所有步骤结合，原行列式为：
$\begin{aligned}\left|\begin{pmatrix} A & B \\ C & D \end{pmatrix}\right| &= |A| \cdot |A^{-1}| \cdot |A D - C B| \\
&= |I| \cdot |A D - C B| \\
&= |DA - CB|.
\end{aligned}$