题目
已知 CB, CB,求 CB
已知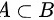 ,
,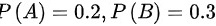 ,求
,求
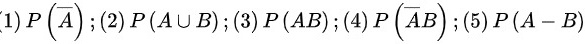
题目解答
答案
(1)由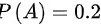 可知:
可知: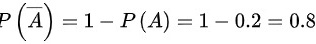
(2)由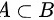 可知
可知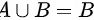 ,因而
,因而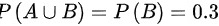
(3)由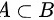 ,可知
,可知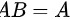 ,因而
,因而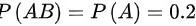
(4)由公式可得: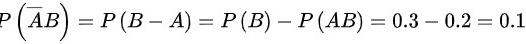
(5)由公式可得: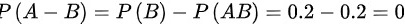
解析
步骤 1:求 $P(\overline{A})$
由概率论中的补事件概率公式,$P(\overline{A})=1-P(A)$,代入已知的 $P(A)=0.2$,得到 $P(\overline{A})=1-0.2=0.8$。
步骤 2:求 $P(A\cup B)$
由题设条件 $g p$,即 $A$ 和 $B$ 是互斥事件,所以 $A\cup B=B$,因此 $P(A\cup B)=P(B)=0.3$。
步骤 3:求 $P(AB)$
由题设条件 $g p$,即 $A$ 和 $B$ 是互斥事件,所以 $AB=A$,因此 $P(AB)=P(A)=0.2$。
步骤 4:求 $P(\overline{AB})$
由公式 $P(\overline{AB})=P(B-A)=P(B)-P(AB)$,代入已知的 $P(B)=0.3$ 和 $P(AB)=0.2$,得到 $P(\overline{AB})=0.3-0.2=0.1$。
步骤 5:求 $P(A-B)$
由公式 $P(A-B)=P(A)-P(AB)$,代入已知的 $P(A)=0.2$ 和 $P(AB)=0.2$,得到 $P(A-B)=0.2-0.2=0$。
由概率论中的补事件概率公式,$P(\overline{A})=1-P(A)$,代入已知的 $P(A)=0.2$,得到 $P(\overline{A})=1-0.2=0.8$。
步骤 2:求 $P(A\cup B)$
由题设条件 $g p$,即 $A$ 和 $B$ 是互斥事件,所以 $A\cup B=B$,因此 $P(A\cup B)=P(B)=0.3$。
步骤 3:求 $P(AB)$
由题设条件 $g p$,即 $A$ 和 $B$ 是互斥事件,所以 $AB=A$,因此 $P(AB)=P(A)=0.2$。
步骤 4:求 $P(\overline{AB})$
由公式 $P(\overline{AB})=P(B-A)=P(B)-P(AB)$,代入已知的 $P(B)=0.3$ 和 $P(AB)=0.2$,得到 $P(\overline{AB})=0.3-0.2=0.1$。
步骤 5:求 $P(A-B)$
由公式 $P(A-B)=P(A)-P(AB)$,代入已知的 $P(A)=0.2$ 和 $P(AB)=0.2$,得到 $P(A-B)=0.2-0.2=0$。