6.求阿基米德螺线 rho =atheta (agt 0) 相应于 leqslant theta leqslant 2pi 的一段弧长.
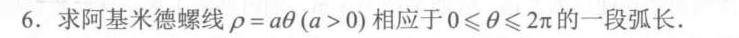
题目解答
答案
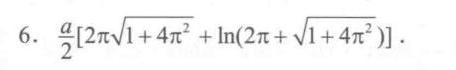
解析
考查要点:本题主要考查极坐标下曲线弧长的计算,涉及积分法的应用。
解题核心思路:
- 极坐标弧长公式:弧长公式为 $\int_{\theta_1}^{\theta_2} \sqrt{\rho^2 + \left( \frac{d\rho}{d\theta} \right)^2} \, d\theta$。
- 代入具体表达式:将阿基米德螺线 $\rho = a\theta$ 代入公式,化简被积函数。
- 积分计算:通过分部积分或查积分表求解 $\int \sqrt{\theta^2 + 1} \, d\theta$,注意上下限代入。
破题关键点:
- 正确应用弧长公式,避免遗漏 $\frac{d\rho}{d\theta}$ 的平方项。
- 积分技巧:处理 $\sqrt{\theta^2 + 1}$ 的积分时,需熟练运用分部积分或积分公式。
步骤1:写出极坐标弧长公式
极坐标下曲线弧长公式为:
$L = \int_{0}^{2\pi} \sqrt{\rho^2 + \left( \frac{d\rho}{d\theta} \right)^2} \, d\theta$
步骤2:代入阿基米德螺线表达式
已知 $\rho = a\theta$,则 $\frac{d\rho}{d\theta} = a$。代入公式得:
$L = \int_{0}^{2\pi} \sqrt{(a\theta)^2 + a^2} \, d\theta = a \int_{0}^{2\pi} \sqrt{\theta^2 + 1} \, d\theta$
步骤3:计算积分 $\int \sqrt{\theta^2 + 1} \, d\theta$
使用分部积分法或积分公式:
$\int \sqrt{\theta^2 + 1} \, d\theta = \frac{\theta}{2} \sqrt{\theta^2 + 1} + \frac{1}{2} \ln \left( \theta + \sqrt{\theta^2 + 1} \right) + C$
步骤4:代入上下限并化简
将上下限 $\theta = 2\pi$ 和 $\theta = 0$ 代入积分结果:
$\begin{aligned}L &= a \left[ \frac{2\pi}{2} \sqrt{(2\pi)^2 + 1} + \frac{1}{2} \ln \left( 2\pi + \sqrt{(2\pi)^2 + 1} \right) \right] \\&= \frac{a}{2} \left[ 2\pi \sqrt{1 + 4\pi^2} + \ln \left( 2\pi + \sqrt{1 + 4\pi^2} \right) \right]\end{aligned}$