题目
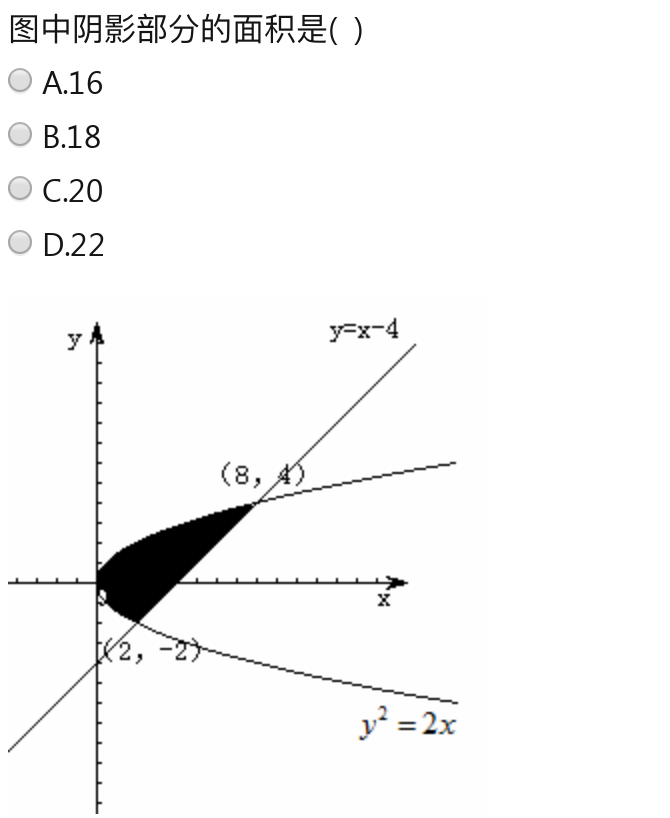
图中阴影部分的面积是 ()-|||-bigcirc A.16-|||-bigcirc B.18-|||-bigcirc C.20-|||-bigcirc D.22
题目解答
答案

解析
步骤 1:联立方程求交点
联立方程 $\left \{ \begin{matrix} y=x-4\\ {y}^{2}=2x\end{matrix} \right.$ ,解得 y=-2 或 y=4 ,即交点为 (-2, -6) 和 (8, 4)。
步骤 2:计算阴影部分面积
阴影部分的面积为曲线 $y^2 = 2x$ 和直线 $y = x - 4$ 之间的区域,可以表示为积分 ${\int }_{-2}^{4}{(y+4-\dfrac {{y}^{2}}{2})dy}$。
步骤 3:计算积分
计算积分 ${\int }_{-2}^{4}{(y+4-\dfrac {{y}^{2}}{2})dy}$,得到 $(-\dfrac {{y}^{3}}{6}+\dfrac {1}{2}{y}^{2}+4y){y}_{-2}^{4} = 18$。
联立方程 $\left \{ \begin{matrix} y=x-4\\ {y}^{2}=2x\end{matrix} \right.$ ,解得 y=-2 或 y=4 ,即交点为 (-2, -6) 和 (8, 4)。
步骤 2:计算阴影部分面积
阴影部分的面积为曲线 $y^2 = 2x$ 和直线 $y = x - 4$ 之间的区域,可以表示为积分 ${\int }_{-2}^{4}{(y+4-\dfrac {{y}^{2}}{2})dy}$。
步骤 3:计算积分
计算积分 ${\int }_{-2}^{4}{(y+4-\dfrac {{y}^{2}}{2})dy}$,得到 $(-\dfrac {{y}^{3}}{6}+\dfrac {1}{2}{y}^{2}+4y){y}_{-2}^{4} = 18$。