题目

四阶行列式中含有因子_(11)(a)_(23)的项为_(11)(a)_(23). A.对B.错

四阶行列式中含有因子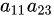的项为.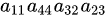

 A.对

B.错

题目解答

答案

四阶行列式的一般项是由位于不同行、不同列的4个元素的乘积组成的，并且这些元素在排列上满足逆序数为偶数（或称为偶排列）的条件。

考虑因子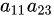，这两个元素已经占据了第1行第1列和第2行第3列的位置。为了找到含有这两个因子的项，我们需要从剩下的元素（即第3行和第4行的元素，以及第1列和第3列之外的元素）中选择两个元素，使得这四个元素构成一个偶排列。

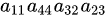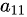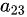然而，给出的项中，虽然包含了和，但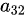并不在剩下的可选元素中（因为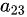已经占据了第2行第3列的位置，所以第3列只剩下第1行和第4行的元素可选），同时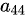虽然可选，但与其他元素的组合并不满足题目中“含有因子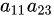”的特定要求下的唯一性。

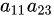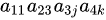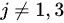实际上，如果我们按照行列式的定义来构造含有的项，并且要求这四个元素来自不同的行和列，那么一个可能的项是，其中且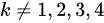（但注意在四阶行列式中，k只能取2或4，因为其他列已经被占据了）。然而，由于k不能取4（因为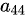已经被用于与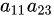组合，但这并不符合题目给出的特定项），所以k只能取2，但这会导致与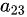在同一列，违反行列式的定义。因此，我们需要从第3行选择除了第2列之外的元素（即第1列或第4列的元素）与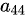组合。

但无论如何，题目给出的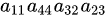并不是四阶行列式中唯一或特定的含有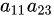的项，且从行列式的定义来看，这个组合并不满足所有元素来自不同行和列的条件（因为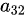与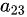在同一列）。

因此，题目中的说法“四阶行列式中含有因子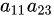的项为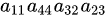”是错误的。

故答案为：B. 错。

解析

考查要点：四阶行列式的一般项构成条件，即元素必须位于不同行、不同列，并且排列的逆序数为偶数（偶排列）。

解题核心思路：

  1. 行列式项的构成：四阶行列式中的每一项都是四个元素的乘积，且每个元素来自不同行、不同列。
  2. 排列的奇偶性：排列的逆序数为偶数时，对应项符号为正；奇数时为负。
  3. 关键矛盾点：题目中给出的项是否唯一满足“包含因子$a_{11}a_{23}$”的条件？需验证是否存在其他可能的项。

破题关键：

  • 验证列的唯一性：若$a_{11}$和$a_{23}$已占据第1列和第3列，则剩余元素需从第2列和第4列中选择。
  • 构造其他可能项：若存在其他满足条件的项，则题目中的说法错误。

步骤1：分析题目给出的项

题目中的项为$a_{11}a_{23}a_{32}a_{44}$，其列索引为$1,3,2,4$，对应排列$(1,3,2,4)$。

  • 逆序数计算：排列$(1,3,2,4)$的逆序数为$1$（仅$3>2$），为奇排列，符号为负。
  • 行列位置：元素来自不同行、不同列，满足行列式项的基本条件。

步骤2：寻找其他可能项

剩余列需为第2列和第4列，剩余行需为第3行和第4行。

  • 构造新项：若选择$a_{34}$（第3行第4列）和$a_{42}$（第4行第2列），则项为$a_{11}a_{23}a_{34}a_{42}$。
  • 排列验证：列索引为$1,3,4,2$，对应排列$(1,3,4,2)$，逆序数为$2$（$3>2$和$4>2$），为偶排列，符号为正。
  • 结论：存在另一项$a_{11}a_{23}a_{34}a_{42}$，同样包含$a_{11}a_{23}$。

步骤3：判断题目说法的正确性

题目中认为“唯一含有$a_{11}a_{23}$的项是$a_{11}a_{44}a_{32}a_{23}$”，但实际存在另一项$a_{11}a_{23}a_{34}a_{42}$，因此题目说法错误。