题目
设(x)=(x)^2 (x)=x-1,求复合函数(x)=(x)^2 (x)=x-1,____ .(x)=(x)^2 (x)=x-1,(x)=(x)^2 (x)=x-1,(x)=(x)^2 (x)=x-1,(x)=(x)^2 (x)=x-1,
设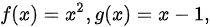 求复合函数
求复合函数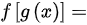 ____ .
____ .
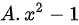
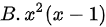
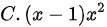
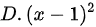
题目解答
答案
解:由题可知, 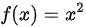 ,
, 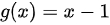 , 则
, 则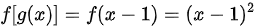 ,
,
故选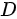 .
.
解析
步骤 1:理解复合函数的概念
复合函数$f(g(x))$表示先将$x$代入$g(x)$中,得到$g(x)$的值,再将$g(x)$的值代入$f(x)$中,得到$f(g(x))$的值。
步骤 2:代入$g(x)$到$f(x)$中
已知$f(x)={x}^{2}$,$g(x)=x-1$,则$f(g(x))=f(x-1)$。
步骤 3:计算$f(g(x))$
将$x-1$代入$f(x)={x}^{2}$中,得到$f(g(x))={(x-1)}^{2}$。
复合函数$f(g(x))$表示先将$x$代入$g(x)$中,得到$g(x)$的值,再将$g(x)$的值代入$f(x)$中,得到$f(g(x))$的值。
步骤 2:代入$g(x)$到$f(x)$中
已知$f(x)={x}^{2}$,$g(x)=x-1$,则$f(g(x))=f(x-1)$。
步骤 3:计算$f(g(x))$
将$x-1$代入$f(x)={x}^{2}$中,得到$f(g(x))={(x-1)}^{2}$。