16.两台车床加工同样的零件,第一台出现不合格品的概率是0.03,第二台出现不合格品的概率是0.06,加工出来的零件放在一起,并且已知第一台加工的零件数比第二台加工的零件数多一倍.(1)求任取一个零件是合格品的概率;(2)如果取出的零件是不合格品,求它是由第二台车床加工的概率.
16.两台车床加工同样的零件,第一台出现不合格品的概率是0.03,第二台出现不合格品的概率是0.06,加工出来的零件放在一起,并且已知第一台加工的零件数比第二台加工的零件数多一倍.
(1)求任取一个零件是合格品的概率;
(2)如果取出的零件是不合格品,求它是由第二台车床加工的概率.
题目解答
答案
记事件A为 取到第一台车床加工的零件 即P(A)=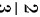 记事件B为 取到合格品
记事件B为 取到合格品
(1)用全概率公式
P(B)=P(A)P(B|A)+P(A‾)P(B|A‾)=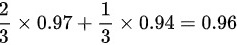
(2)用贝叶斯公式
P(A‾|B‾)=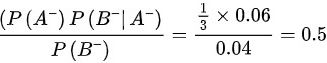
解析
考查要点:本题主要考查全概率公式和贝叶斯公式的应用,涉及条件概率的理解与计算。
解题核心思路:
- 确定各事件的概率关系:根据题目中两台车床加工零件数的比例,确定取到各车床零件的概率;结合各车床不合格品率,建立条件概率关系。
- 全概率公式:用于计算任取一个零件的合格概率,需综合两台车床的贡献。
- 贝叶斯公式:用于在已知不合格品的条件下,反推其来自第二台车床的概率,需注意分母是不合格品的总概率。
破题关键点:
- 明确比例关系:第一台加工的零件数是第二台的两倍,因此取到第一台零件的概率为$\dfrac{2}{3}$,第二台为$\dfrac{1}{3}$。
- 区分合格与不合格的条件概率:第一台合格概率为$0.97$,第二台合格概率为$0.94$;不合格概率分别为$0.03$和$0.06$。
第(1)题
目标:计算任取一个零件是合格品的概率。
定义事件
- 事件$A$:取到第一台车床加工的零件,概率$P(A) = \dfrac{2}{3}$。
- 事件$\overline{A}$:取到第二台车床加工的零件,概率$P(\overline{A}) = \dfrac{1}{3}$。
- 事件$B$:零件是合格品。
应用全概率公式
$P(B) = P(A)P(B|A) + P(\overline{A})P(B|\overline{A})$
代入数值
- 第一台合格概率:$P(B|A) = 1 - 0.03 = 0.97$
- 第二台合格概率:$P(B|\overline{A}) = 1 - 0.06 = 0.94$
$P(B) = \dfrac{2}{3} \times 0.97 + \dfrac{1}{3} \times 0.94 = 0.96$
第(2)题
目标:已知零件是不合格品,求它由第二台车床加工的概率。
定义事件
- 事件$\overline{B}$:零件是不合格品。
- 目标概率:$P(\overline{A}|\overline{B})$
应用贝叶斯公式
$P(\overline{A}|\overline{B}) = \dfrac{P(\overline{B}|\overline{A})P(\overline{A})}{P(\overline{B})}$
计算分母$P(\overline{B})$
利用全概率公式:
$P(\overline{B}) = P(A)P(\overline{B}|A) + P(\overline{A})P(\overline{B}|\overline{A})$
代入数值:
$P(\overline{B}) = \dfrac{2}{3} \times 0.03 + \dfrac{1}{3} \times 0.06 = 0.04$
代入贝叶斯公式
$P(\overline{A}|\overline{B}) = \dfrac{0.06 \times \dfrac{1}{3}}{0.04} = \dfrac{0.02}{0.04} = 0.5$