题目
证明:函数 f(x)=|x| 当 arrow 0 时极限为零.
证明: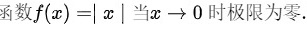
题目解答
答案
解:由题
∵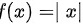
∴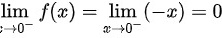
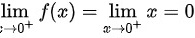
而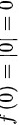
∴根据极限的定义,函数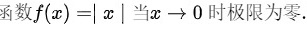
解析
考查要点:本题主要考查函数在某一点的极限存在性证明,特别是涉及绝对值函数的左右极限计算。
解题核心思路:
对于分段函数或含有绝对值的函数,分左右极限讨论是关键。当$x \rightarrow 0$时,需分别考虑$x$从左侧(负方向)和右侧(正方向)趋近于0的情况,验证左右极限是否相等,从而确定极限是否存在。
破题关键点:
- 拆解绝对值表达式:当$x < 0$时,$|x| = -x$;当$x \geq 0$时,$|x| = x$。
- 分别计算左右极限:左极限($x \rightarrow 0^-$)和右极限($x \rightarrow 0^+$)的值是否相等。
- 结合极限定义:若左右极限相等,则极限存在且等于该值。
步骤1:计算左极限($x \rightarrow 0^-$)
当$x$从左侧趋近于0时,$x$为负数,因此:
$|x| = -x$
此时左极限为:
$\lim_{x \rightarrow 0^-} f(x) = \lim_{x \rightarrow 0^-} (-x) = 0$
步骤2:计算右极限($x \rightarrow 0^+$)
当$x$从右侧趋近于0时,$x$为正数,因此:
$|x| = x$
此时右极限为:
$\lim_{x \rightarrow 0^+} f(x) = \lim_{x \rightarrow 0^+} x = 0$
步骤3:验证左右极限相等
由于左极限和右极限均为0,根据极限定义,函数$f(x)$在$x \rightarrow 0$时的极限存在且等于0。
步骤4(补充):验证函数值(非必需但可增强结论)
函数在$x=0$处的值为:
$f(0) = |0| = 0$
这表明函数在$x=0$处连续,但题目仅要求证明极限,因此此步骤可省略。