(int )_(e)^-xcos xdx=____________
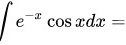 ____________
____________
题目解答
答案
根据分部积分
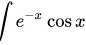
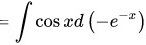
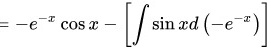
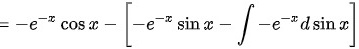
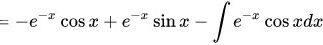
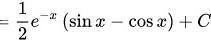
(C为任意常数)
综上,本题答案为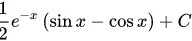
解析
考查要点:本题主要考查分部积分法的应用,特别是处理含有指数函数和三角函数乘积的积分问题。需要学生掌握分部积分法的重复使用以及通过代数方法解方程得到最终结果。
解题核心思路:
对于形如 $\int e^{ax} \cos(bx) dx$ 或 $\int e^{ax} \sin(bx) dx$ 的积分,通常需要两次分部积分,并将得到的表达式重新整理,解关于原积分的方程。本题中,指数函数为 $e^{-x}$,三角函数为 $\cos x$,因此需要两次分部积分后,通过代数变形求解。
破题关键点:
- 正确选择分部积分中的 $u$ 和 $dv$,通常优先将三角函数设为 $u$,指数函数设为 $dv$。
- 两次分部积分后,将原积分项移到等式另一边,合并同类项后解方程。
- 注意积分常数 $C$ 的添加,特别是在不定积分中不可遗漏。
题目:计算不定积分 $\int e^{-x} \cos x \, dx$。
第一步:第一次分部积分
设 $u = \cos x$,则 $du = -\sin x \, dx$;
设 $dv = e^{-x} dx$,则 $v = -e^{-x}$。
根据分部积分公式 $\int u \, dv = uv - \int v \, du$,得:
$\begin{aligned}\int e^{-x} \cos x \, dx &= -e^{-x} \cos x - \int (-e^{-x})(-\sin x) \, dx \\&= -e^{-x} \cos x - \int e^{-x} \sin x \, dx.\end{aligned}$
第二步:第二次分部积分
对 $\int e^{-x} \sin x \, dx$ 再次应用分部积分:
设 $u = \sin x$,则 $du = \cos x \, dx$;
设 $dv = e^{-x} dx$,则 $v = -e^{-x}$。
则:
$\begin{aligned}\int e^{-x} \sin x \, dx &= -e^{-x} \sin x - \int (-e^{-x}) \cos x \, dx \\&= -e^{-x} \sin x + \int e^{-x} \cos x \, dx.\end{aligned}$
第三步:代入并解方程
将第二次分部积分的结果代入第一步的表达式:
$\begin{aligned}\int e^{-x} \cos x \, dx &= -e^{-x} \cos x - \left( -e^{-x} \sin x + \int e^{-x} \cos x \, dx \right) \\&= -e^{-x} \cos x + e^{-x} \sin x - \int e^{-x} \cos x \, dx.\end{aligned}$
将等式两边的 $\int e^{-x} \cos x \, dx$ 移到左边:
$2 \int e^{-x} \cos x \, dx = e^{-x} (\sin x - \cos x) + C.$
最终解得:
$\int e^{-x} \cos x \, dx = \frac{1}{2} e^{-x} (\sin x - \cos x) + C.$