题目
四.判断题 (共5题,10.0分)-|||-1.(判断题2.0分)-|||-矩阵A、B满足 =0, 且 A≠0, 则 =0.-|||-A 对-|||-B 错

题目解答
答案
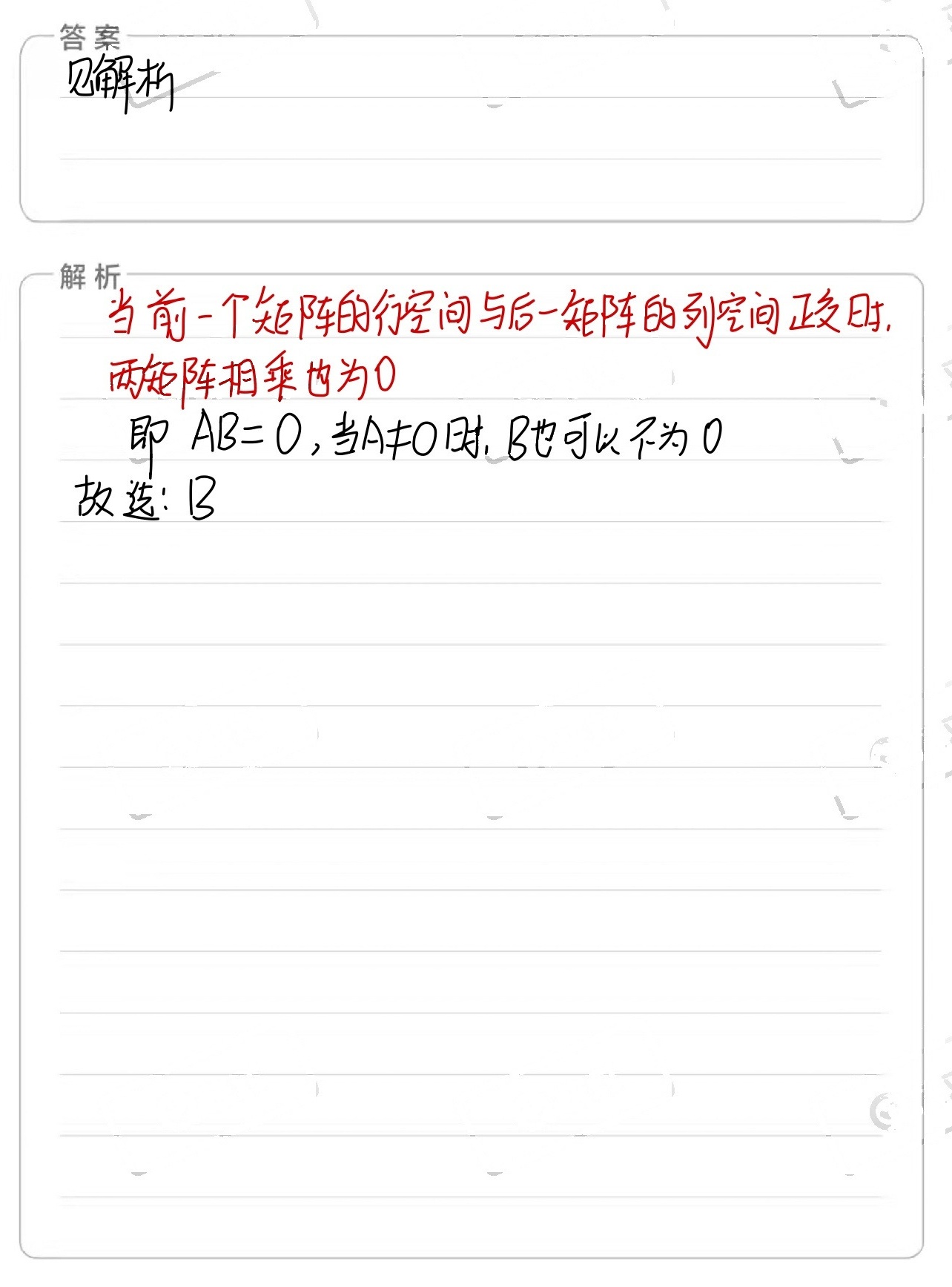
解析
本题主要考察矩阵乘法的性质,判断当$AB=O$且$A\neq O$时,$B$是否一定为$O$。
关键分析:
矩阵乘法中,$AB=O\\)(零矩阵))并不意味着\(B$必须是零矩阵。反例如下:
设$A=\begin{pmatrix}1&0\\0&0\end{pmatrix}$(非零矩阵,第二行全为0),$B=\begin{pmatrix}0&0\\0&1\end{pmatrix}$(非零矩阵,第二列全为1),则:
$AB=\begin{pmatrix1×0+0×0&1×0+0×1\\0×0+0×0&0×0+0×1\end{pmatrix}=\begin{pmatrix}0&0\\0&0\end{pmatrix}=O$
显然$A\neq O$、$B\neq O$,但$AB=O$,因此原命题错误。