求直线 ) 5x-3y+3z-9=0 3x-2y+z-1=0 . 的-|||-夹角的余弦.
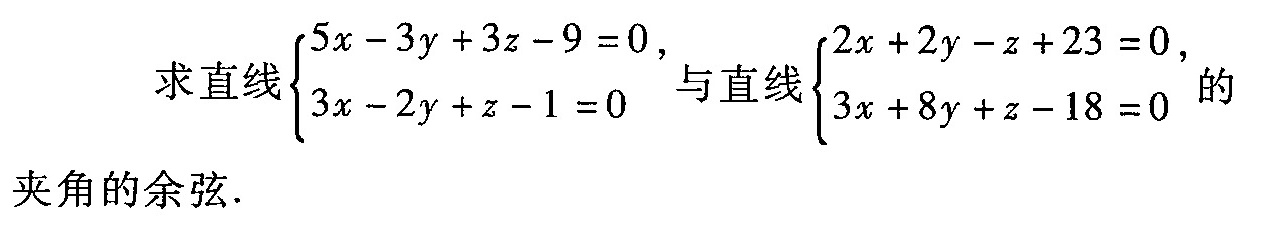
题目解答
答案
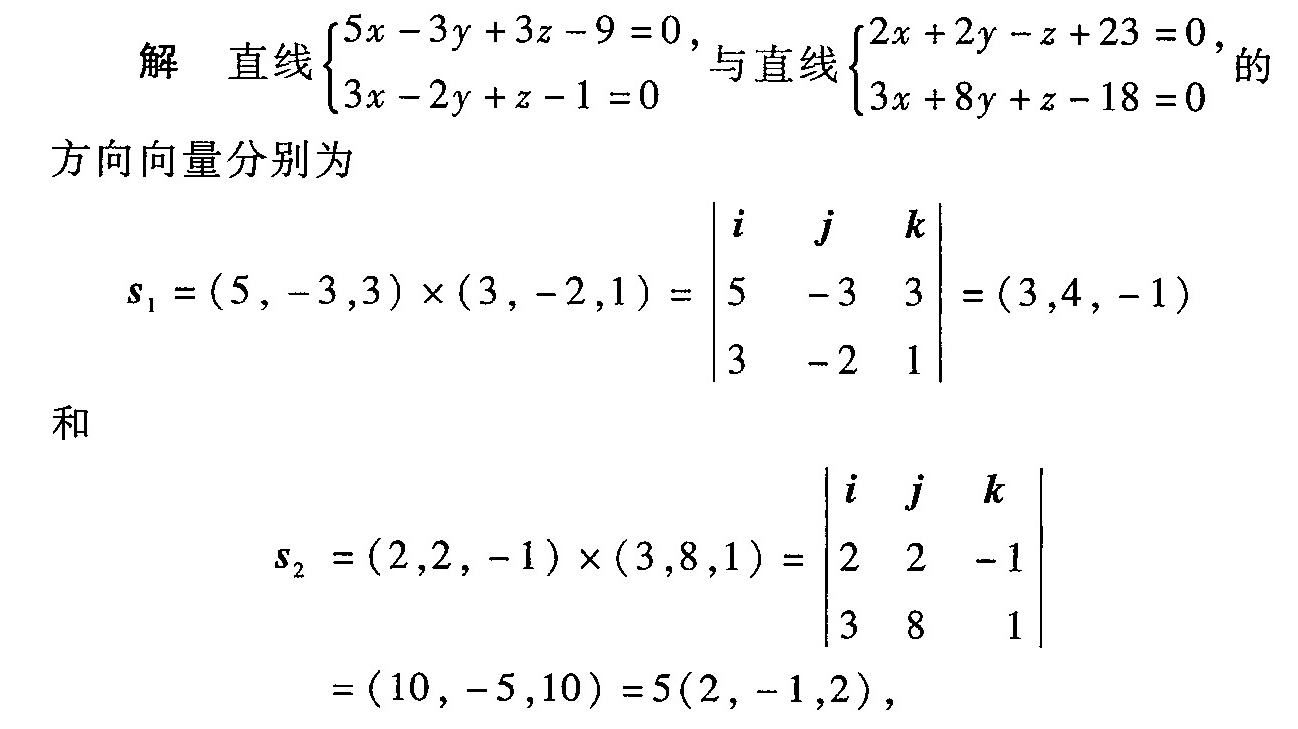
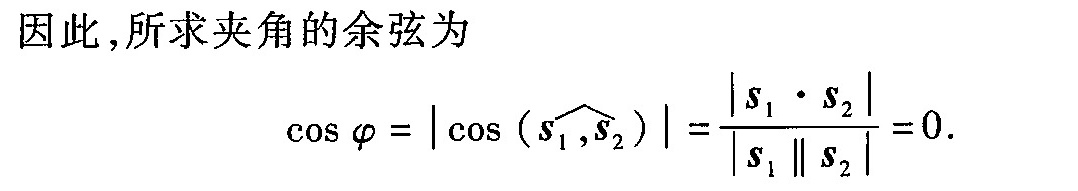
解析
考查要点:本题主要考查空间直线方向向量的求解方法,以及利用向量点积公式计算两直线夹角的余弦值。
解题核心思路:
- 确定直线的方向向量:每条直线由两个平面方程确定,其方向向量为两平面法向量的叉乘结果。
- 计算方向向量的点积与模长:通过两方向向量的点积公式和模长公式,代入计算夹角的余弦值。
- 关键点:叉乘运算的准确性,点积结果为零时的几何意义(两向量垂直)。
第一步:求第一条直线的方向向量 $\mathbf{s_1}$
第一条直线由平面 $5x-3y+3z-9=0$ 和 $3x-2y+z-1=0$ 确定,法向量分别为 $\mathbf{n_1}=(5,-3,3)$ 和 $\mathbf{n_2}=(3,-2,1)$。方向向量 $\mathbf{s_1}$ 为两法向量的叉乘:
$\mathbf{s_1} = \mathbf{n_1} \times \mathbf{n_2} =
\begin{vmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k} \\5 & -3 & 3 \\3 & -2 & 1\end{vmatrix} = (3,4,-1)$
第二步:求第二条直线的方向向量 $\mathbf{s_2}$
第二条直线由平面 $2x+2y-z+23=0$ 和 $3x+8y+z-18=0$ 确定,法向量分别为 $\mathbf{n_3}=(2,2,-1)$ 和 $\mathbf{n_4}=(3,8,1)$。方向向量 $\mathbf{s_2}$ 为两法向量的叉乘:
$\mathbf{s_2} = \mathbf{n_3} \times \mathbf{n_4} =
\begin{vmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k} \\2 & 2 & -1 \\3 & 8 & 1\end{vmatrix} = (10,-5,10) = 5(2,-1,2)$
第三步:计算夹角的余弦值
两向量点积为:
$\mathbf{s_1} \cdot \mathbf{s_2} = 3 \cdot 10 + 4 \cdot (-5) + (-1) \cdot 10 = 30 - 20 - 10 = 0$
两向量模长分别为:
$|\mathbf{s_1}| = \sqrt{3^2 + 4^2 + (-1)^2} = \sqrt{26}, \quad |\mathbf{s_2}| = \sqrt{10^2 + (-5)^2 + 10^2} = \sqrt{225} = 15$
因此,夹角的余弦值为:
$\cos \varphi = \frac{|\mathbf{s_1} \cdot \mathbf{s_2}|}{|\mathbf{s_1}| \cdot |\mathbf{s_2}|} = \frac{0}{\sqrt{26} \cdot 15} = 0$