下列方阵中,不可逆的是().A). 1 6-|||-3 2-|||-2-|||-6A). 1 6-|||-3 2-|||-2-|||-6A). 1 6-|||-3 2-|||-2-|||-6A). 1 6-|||-3 2-|||-2-|||-6
下列方阵中,不可逆的是().
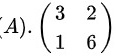
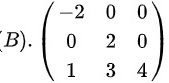
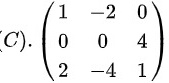
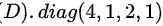
题目解答
答案
对于 ,
,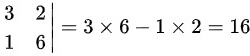 ;对于
;对于 选项,
选项,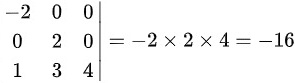 ;对于
;对于 选项,因为行列式的值等于行列式的某行(列)元素分别乘其相应的代数余子式后再求和,按第二行展开可得
选项,因为行列式的值等于行列式的某行(列)元素分别乘其相应的代数余子式后再求和,按第二行展开可得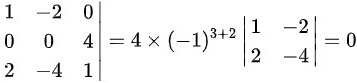 ;对于
;对于 选项,
选项,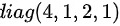 表示对角线元素为
表示对角线元素为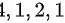 ,其余元素全为零的方阵,故其行列式为
,其余元素全为零的方阵,故其行列式为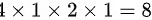 ;因为当矩阵不可逆时,其行列式等于零,在四个选项中,只有选项的行列式等于零,所以答案选择
;因为当矩阵不可逆时,其行列式等于零,在四个选项中,只有选项的行列式等于零,所以答案选择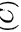 选项。
选项。
解析
考查要点:本题主要考查矩阵可逆的判定条件,即行列式是否为零。若矩阵的行列式为零,则该矩阵不可逆。
解题核心思路:
- 计算每个选项的行列式,判断其是否为零。
- 关键点在于正确展开行列式,尤其是选项C的行列式计算,需注意代数余子式的符号和展开方法。
选项分析
选项(A)
矩阵为:
$\begin{pmatrix}3 & 2 \\1 & 6\end{pmatrix}$
行列式计算:
$\begin{vmatrix}3 & 2 \\1 & 6\end{vmatrix}
= 3 \times 6 - 1 \times 2 = 16 \neq 0$
结论:可逆。
选项(B)
矩阵为:
$\begin{pmatrix}-2 & 0 & 0 \\0 & 2 & 0 \\1 & 3 & 4\end{pmatrix}$
行列式计算(按第一列展开):
$\begin{vmatrix}-2 & 0 & 0 \\0 & 2 & 0 \\1 & 3 & 4\end{vmatrix}
= -2 \times \begin{vmatrix} 2 & 0 \\ 3 & 4 \end{vmatrix} = -2 \times (2 \times 4 - 0 \times 3) = -16 \neq 0$
结论:可逆。
选项(C)
矩阵为:
$\begin{pmatrix}1 & -2 & 0 \\0 & 0 & 4 \\2 & -4 & 1\end{pmatrix}$
行列式计算(按第二行展开):
$\begin{vmatrix}1 & -2 & 0 \\0 & 0 & 4 \\2 & -4 & 1\end{vmatrix}
= 0 \cdot (-1)^{2+1} \cdot M_{21} + 0 \cdot (-1)^{2+2} \cdot M_{22} + 4 \cdot (-1)^{2+3} \cdot \begin{vmatrix} 1 & -2 \\ 2 & -4 \end{vmatrix}$
其中:
$\begin{vmatrix} 1 & -2 \\ 2 & -4 \end{vmatrix} = 1 \times (-4) - (-2) \times 2 = -4 + 4 = 0$
因此:
$\text{行列式} = 4 \cdot (-1)^5 \cdot 0 = 0$
结论:不可逆。
选项(D)
矩阵为对角矩阵:
$\text{diag}(4, 1, 2, 1)$
行列式计算:
$4 \times 1 \times 2 \times 1 = 8 \neq 0$
结论:可逆。