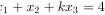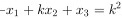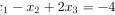题目
设有线性方程组 https:/img.zuoyebang.cc/zyb_b4f22457fcdd5def491e4eb46a62ac9d.jpg+(x)_(2)+k(x)_(3)=4 https:/img.zuoyebang.cc/zyb_f6265e1a3acd93710c9defcc4f21d073.jpg+(x)_(2)+k(x)_(3)=4 https:/img.zuoyebang.cc/zyb_d03c4be000d5b7114d179543d1c0afe5.jpg+(x)_(2)+k(x)_(3)=4 ,问k取何值时,方程组 (1)有唯一解; (2)无解; (3)有无穷多个解?并在有无穷多解时求其通解.
设有线性方程组
|
|
|
(1)有唯一解;
(2)无解;
(3)有无穷多个解?并在有无穷多解时求其通解.
题目解答
答案

解析
步骤 1:写出增广矩阵
将方程组写成增广矩阵的形式,我们得到:
$B=\left (\begin{matrix} 1& 1& k& 4\\ -1& k& 1& {k}^{2}\\ 1& -1& 2& -4\end{matrix} ) \right.$
步骤 2:进行行变换
我们对增广矩阵进行行变换,以简化它。首先,将第一行加到第二行和第三行,得到:
$B=\left (\begin{matrix} 1& 1& k& 4\\ 0& k+1& k+1& {k}^{2}+4\\ 0& 0& 2+k& 0\end{matrix} ) \right.$
步骤 3:进一步简化
接下来,我们继续简化矩阵。将第二行乘以$\frac{1}{k+1}$(假设$k\neq -1$),然后将第二行乘以$-1$加到第一行,得到:
$B=\left (\begin{matrix} 1& 0& 0& 4\\ 0& 1& 1& \frac{{k}^{2}+4}{k+1}\\ 0& 0& 2+k& 0\end{matrix} ) \right.$
步骤 4:确定解的情况
现在,我们根据$k$的值来确定方程组的解的情况。
- 当$k\neq -1$且$k\neq -2$时,方程组有唯一解。
- 当$k=-1$时,方程组无解,因为此时第三行变为$0=0$,而第二行变为$0=3$,这是矛盾的。
- 当$k=-2$时,方程组有无穷多个解,因为此时第三行变为$0=0$,表示一个自由变量。
步骤 5:求无穷多解时的通解
当$k=-2$时,方程组变为:
${x}_{1}+{x}_{2}-2{x}_{3}=4$
$-{x}_{1}-2{x}_{2}+{x}_{3}=4$
${1}_{1}-{x}_{2}+2{x}_{3}=-4$
简化后得到:
${x}_{1}=4$
${x}_{2}=-2{x}_{3}$
${x}_{3}$为自由变量,所以通解为:
$x=\left (\begin{matrix} 4\\ -2{x}_{3}\\ {x}_{3}\end{matrix} ) \right.$
将方程组写成增广矩阵的形式,我们得到:
$B=\left (\begin{matrix} 1& 1& k& 4\\ -1& k& 1& {k}^{2}\\ 1& -1& 2& -4\end{matrix} ) \right.$
步骤 2:进行行变换
我们对增广矩阵进行行变换,以简化它。首先,将第一行加到第二行和第三行,得到:
$B=\left (\begin{matrix} 1& 1& k& 4\\ 0& k+1& k+1& {k}^{2}+4\\ 0& 0& 2+k& 0\end{matrix} ) \right.$
步骤 3:进一步简化
接下来,我们继续简化矩阵。将第二行乘以$\frac{1}{k+1}$(假设$k\neq -1$),然后将第二行乘以$-1$加到第一行,得到:
$B=\left (\begin{matrix} 1& 0& 0& 4\\ 0& 1& 1& \frac{{k}^{2}+4}{k+1}\\ 0& 0& 2+k& 0\end{matrix} ) \right.$
步骤 4:确定解的情况
现在,我们根据$k$的值来确定方程组的解的情况。
- 当$k\neq -1$且$k\neq -2$时,方程组有唯一解。
- 当$k=-1$时,方程组无解,因为此时第三行变为$0=0$,而第二行变为$0=3$,这是矛盾的。
- 当$k=-2$时,方程组有无穷多个解,因为此时第三行变为$0=0$,表示一个自由变量。
步骤 5:求无穷多解时的通解
当$k=-2$时,方程组变为:
${x}_{1}+{x}_{2}-2{x}_{3}=4$
$-{x}_{1}-2{x}_{2}+{x}_{3}=4$
${1}_{1}-{x}_{2}+2{x}_{3}=-4$
简化后得到:
${x}_{1}=4$
${x}_{2}=-2{x}_{3}$
${x}_{3}$为自由变量,所以通解为:
$x=\left (\begin{matrix} 4\\ -2{x}_{3}\\ {x}_{3}\end{matrix} ) \right.$