题目
求过点M(-2,7,4),且与平面M(-2,7,4)平行的平面方程为M(-2,7,4)M(-2,7,4)M(-2,7,4)M(-2,7,4)M(-2,7,4)M(-2,7,4)M(-2,7,4)M(-2,7,4)M(-2,7,4)
求过点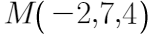 ,且与平面
,且与平面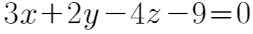 平行的平面方程为
平行的平面方程为
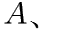
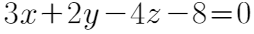
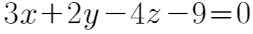
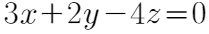
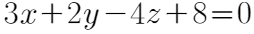
题目解答
答案
D. 3x+2y-4z+8=0
解析
步骤 1:确定平面的法向量
已知平面3x+2y-4z-9=0的法向量为(3,2,-4)。因为所求平面与已知平面平行,所以所求平面的法向量也是(3,2,-4)。
步骤 2:利用点法式方程求平面方程
设所求平面方程为3x+2y-4z+d=0,其中d为待定常数。因为平面过点M(-2,7,4),所以将点M的坐标代入平面方程中求解d。
3(-2)+2(7)-4(4)+d=0
-6+14-16+d=0
d=8
步骤 3:写出所求平面方程
将d=8代入平面方程中,得到所求平面方程为3x+2y-4z+8=0。
已知平面3x+2y-4z-9=0的法向量为(3,2,-4)。因为所求平面与已知平面平行,所以所求平面的法向量也是(3,2,-4)。
步骤 2:利用点法式方程求平面方程
设所求平面方程为3x+2y-4z+d=0,其中d为待定常数。因为平面过点M(-2,7,4),所以将点M的坐标代入平面方程中求解d。
3(-2)+2(7)-4(4)+d=0
-6+14-16+d=0
d=8
步骤 3:写出所求平面方程
将d=8代入平面方程中,得到所求平面方程为3x+2y-4z+8=0。