题目
当__________时，方程组有非零解.（ ）
当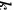
__________时，方程组
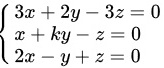有非零解.（ ）
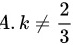
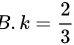
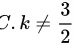
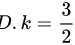
题目解答
答案
由其次线性方程解的判定定理可知：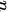
元方程组
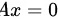有非零解当且仅当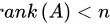
∵方程组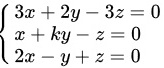的系数矩阵是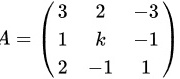
又因为方程组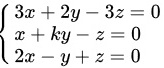有非零解
∴
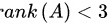
由于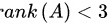当且仅当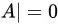
∴
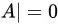
∵由按行展开的行列式计算公式可知：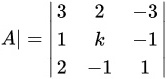
∴
∴
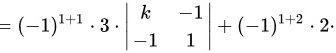
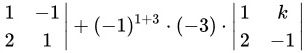
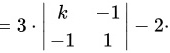
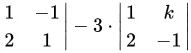
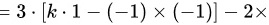
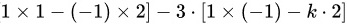
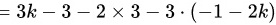
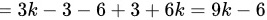
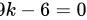
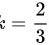
故答案是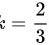：，选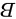
解析
步骤 1：确定方程组有非零解的条件
根据线性代数中的定理，一个齐次线性方程组有非零解的充分必要条件是其系数矩阵的秩小于未知数的个数。对于本题，方程组有三个未知数，因此系数矩阵的秩必须小于3。
步骤 2：计算系数矩阵的行列式
方程组的系数矩阵为：
$$
A = \begin{pmatrix}
3 & 2 & -3 \\
1 & k & -1 \\
2 & -1 & 1
\end{pmatrix}
$$
计算行列式$|A|$：
$$
|A| = 3 \cdot (k \cdot 1 - (-1) \cdot (-1)) - 2 \cdot (1 \cdot 1 - (-1) \cdot 2) - 3 \cdot (1 \cdot (-1) - k \cdot 2)
$$
$$
= 3 \cdot (k - 1) - 2 \cdot (1 + 2) - 3 \cdot (-1 - 2k)
$$
$$
= 3k - 3 - 6 + 3 + 6k
$$
$$
= 9k - 6
$$
步骤 3：确定行列式为0的条件
为了使方程组有非零解，行列式$|A|$必须等于0，即：
$$
9k - 6 = 0
$$
解得：
$$
k = \frac{2}{3}
$$
根据线性代数中的定理，一个齐次线性方程组有非零解的充分必要条件是其系数矩阵的秩小于未知数的个数。对于本题，方程组有三个未知数，因此系数矩阵的秩必须小于3。
步骤 2：计算系数矩阵的行列式
方程组的系数矩阵为：
$$
A = \begin{pmatrix}
3 & 2 & -3 \\
1 & k & -1 \\
2 & -1 & 1
\end{pmatrix}
$$
计算行列式$|A|$：
$$
|A| = 3 \cdot (k \cdot 1 - (-1) \cdot (-1)) - 2 \cdot (1 \cdot 1 - (-1) \cdot 2) - 3 \cdot (1 \cdot (-1) - k \cdot 2)
$$
$$
= 3 \cdot (k - 1) - 2 \cdot (1 + 2) - 3 \cdot (-1 - 2k)
$$
$$
= 3k - 3 - 6 + 3 + 6k
$$
$$
= 9k - 6
$$
步骤 3：确定行列式为0的条件
为了使方程组有非零解，行列式$|A|$必须等于0，即：
$$
9k - 6 = 0
$$
解得：
$$
k = \frac{2}{3}
$$