题目
设A,B为随机事件, (A)=0.7, (A-B)=0.3, 则P(AB)=_______
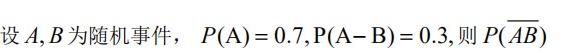
=_______
题目解答
答案
解析
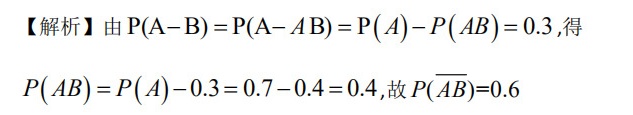
解析
考查要点:本题主要考查事件差的概率计算及事件分解的基本原理。
解题核心思路:利用事件差的概率公式,将事件A分解为互不相交的两部分:A发生且B不发生(即A-B)与A和B同时发生(即AB)。
关键点:明确事件差的定义,即$P(A-B) = P(A) - P(AB)$,并代入已知数值求解。
根据事件差的定义,事件$A-B$表示“A发生但B不发生”,其概率可表示为:
$P(A-B) = P(A) - P(AB)$
将已知条件代入公式:
- $P(A) = 0.7$
- $P(A-B) = 0.3$
代入公式得:
$0.3 = 0.7 - P(AB)$
解得:
$P(AB) = 0.7 - 0.3 = 0.4$